Các bước tính bán kính nguyên tử - Hoá 10

Nguyên tử vô cùng nhỏ nhưng được tạo thành từ các hạt nhỏ hơn, trung hoà về điện.

- Kích thước của nguyên tử là khoảng không gian tạo bởi sự chuyển động của electron. Nếu xem nguyên tử như một khối cầu thì đường kính nguyên tử khoảng 10^-12m => Kích thước của nguyên tử rất nhỏ => Nên thường biểu thị bằng đơn vị picomet (pm), nonomet (nm) hay angstrom (\(\mathop {\rm{A}}\limits^{\rm{0}} \) ).

                                 1pm =10^-12m; 1\(\mathop {\rm{A}}\limits^{\rm{0}} \)= 10^-10m ; 1nm = 10^-9m

a. Đổi các đại lượng: \({\rm{1nm  =  1}}{{\rm{0}}^{ - 9}}{\rm{m  =  1}}{{\rm{0}}^{ - 8}}{\rm{dm  = 1}}{{\rm{0}}^{ - 7}}{\rm{cm}}\); \({\rm{1}}\mathop {\rm{A}}\limits^{\rm{0}}  = {10^{ - 10}}m = {10^{ - 9}}dm = {10^{ - 8}}cm\)

b. Công thức tính:

- Nguyên tử xem như một khối cầu nên thể tích:

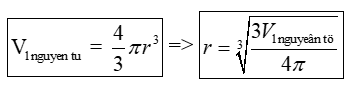
r: bán kính nguyên tử

V 1 nguyên tử: thể tích 1 nguyên tử

* Các công thức tính BKNT và một số vấn đề liên quan:

- Thể tích 1 nguyên tử: \({{\rm{V}}_{{\rm{1nguyen tu}}}}{\rm{  =  }}\frac{{{{\rm{m}}_{{\rm{1 nguyen tu }}}}}}{{\rm{D}}}\)  

D: khối lượng riêng (g/cm3)

m: khối lượng (g) của 1 nguyên tử = 1,6605.10-24

- Thể tích thực một mol nguyên tử   \({{\rm{V}}_{{\rm{thuc 1 mol}}}}{\rm{  =  }}\frac{{{{\rm{V}}_{{\rm{mot mol}}}}{\rm{.x}}}}{{{\rm{100}}}}\)      với x% thể tích thật sự chiếm.

- Thể tích một nguyên tử   \({{\rm{V}}_{{\rm{mot nguyen tu }}}}{\rm{  =  }}\frac{{{{\rm{V}}_{{\rm{thuc mot mol}}}}}}{{6,{{022.10}^{23}}}}\) 

- Bán kính nguyên tử:   \({\rm{r  =  }}\sqrt[{\rm{3}}]{{\frac{{{\rm{3}}{\rm{.M}}{\rm{.1,6605}}{\rm{.1}}{{\rm{0}}^{ - 24}}{\rm{.x}}}}{{{\rm{D}}{\rm{.4}}\pi .100}}}}\)