Cho hình chóp đều $S.ABCD$. Mặt phẳng $\left( \alpha  \right)$ qua $AB$ và vuông góc với mặt phẳng $\left( {SCD} \right)$. Thiết diện tạo bởi $\left( \alpha  \right)$ với hình chóp đã cho là:

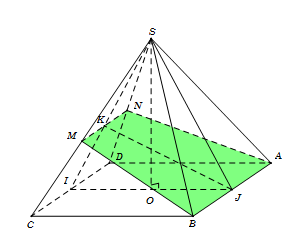
Gọi $I,{\rm{ }}J$ lần lượt là trung điểm của $CD$ và $AB$.

Trong tam giác $SIJ$ kẻ $JK \bot SI$.

Trong tam giác $SIJ$, qua $K$ kẻ đường thẳng song song với $CD$ cắt $SC$ tại $M$, cắt $SD$ tại $N$.

Ta dễ dàng chứng minh được $\left( {ABMN} \right) \bot \left( {SCD} \right)$.

Khi đó thiết diện cần tìm là hình thang $ABMN$.

Vì hình chóp đã cho là hình chóp đều nên $AN = BM$.

Vậy thiết diện là hình thang cân.