Cho hai đường thẳng song song $a$ và $b$, một đường thẳng $c$ không song song với chúng. Có bao nhiêu phép tịnh tiến biến đường thẳng $a$ thành đường thẳng $b$ và biến đường thẳng $c$ thành chính nó?
-
A.
Không có phép nào
-
B.
Có một phép duy nhất
-
C.
Chỉ có hai phép
-
D.
Có vô số phép
Sử dụng tính chất phép tịnh tiến: biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
+) Véc tơ tịnh tiến có giá song song hoặc trùng với đường thẳng thì biến đường thẳng thành chính nó.
+) Véc tơ tịnh tiến có giá cắt đường thẳng thì biến đường thẳng thành đường thẳng song song với nó.
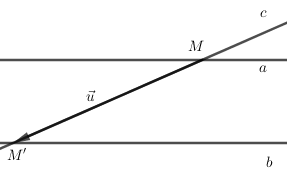
Phép tịnh tiến biến đường thẳng \(c\) thành chính nó và đường thẳng \(c\) cắt cả hai đường thẳng \(a,b\) nên véc tơ tịnh tiến là véc tơ có giá song song hoặc trùng với \(c\).
Từ hình vẽ ta thấy phép tịnh tiến theo véc tơ $\overrightarrow {MM'} $ biến \(a\) thành \(b\) và biến \(c\) thành chính nó.
Có duy nhất một véc tơ thỏa mãn bài toán.
Đáp án : B








Danh sách bình luận