Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): y = x + m – 1 và parabol (P): \(y = {x^2}\). Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ lần lượt là \({x_1}\), \({x_2}\) thỏa mãn: \(4\left( {\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}}} \right) - {x_1}{x_2} + 3 = 0\).
Lập phương trình hoành độ giao điểm của (d) và (P). Áp dụng điều kiện của \(\Delta \) để phương trình có hai nghiệm và áp dụng định lí Viète để biến đổi \(4\left( {\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}}} \right) - {x_1}{x_2} + 3 = 0\), tìm m.
Phương trình hoành độ giao điểm của (d) và (P) là:
\(x + m - 1 = {x^2}\)
\( \Leftrightarrow {x^2} - x - m + 1 = 0\) (*)
Để (d) cắt parabol (P) tại hai điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt.
Khi đó \(\Delta = {b^2} - 4ac = {( - 1)^2} - 4.1.( - m + 1) = 1 + 4m - 4 = 4m - 3 > 0 \Leftrightarrow m > \frac{3}{4}\).
Áp dụng định lí Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a} = - \frac{{ - 1}}{1} = 1\\{x_1}{x_2} = \frac{c}{a} = \frac{{ - m + 1}}{1} = - m + 1\end{array} \right.\)
Theo đề bài: \(4\left( {\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}}} \right) - {x_1}{x_2} + 3 = 0\)
\( \Leftrightarrow 4.\frac{{{x_2} + {x_1}}}{{{x_1}{x_2}}} - {x_1}{x_2} + 3 = 0\)
\( \Leftrightarrow 4.\frac{1}{{ - m + 1}} - ( - m + 1) + 3 = 0\) (ĐK: \(m \ne 1\))
\( \Leftrightarrow 4 - {( - m + 1)^2} + 3( - m + 1) = 0\)
\( \Leftrightarrow 4 - ({m^2} - 2m + 1) - 3m + 3 = 0\)
\( \Leftrightarrow - {m^2} - m + 6 = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}m = - 3\\m = 2\end{array} \right.\)
Mà \(m > \frac{3}{4}\) nên chỉ có m = 2 thỏa mãn.
Vậy m = 2 là giá trị cần tìm.
Để giải quyết bài toán tìm tham số m sao cho đường thẳng và parabol cắt nhau tại hai điểm phân biệt thỏa mãn một điều kiện liên quan đến hoành độ giao điểm, chúng ta áp dụng các lí thuyết cơ bản sau:
1. Phương trình hoành độ giao điểm:
Đây là bước đầu tiên để tìm tọa độ các điểm mà đường thẳng và parabol giao nhau. Ta cho hai biểu thức của y bằng nhau. Cụ thể, từ phương trình đường thẳng y = x + m – 1 và parabol $y = {x^2}$, ta thiết lập phương trình $x + m - 1 = {x^2}$. Bằng cách chuyển vế, ta thu được một phương trình bậc hai theo biến x, có dạng $ax^2 + bx + c = 0$. Trong bài toán này, phương trình đó là ${x^2} - x - m + 1 = 0$ (*), với a = 1, b = -1, c = -m + 1. Các nghiệm của phương trình này chính là hoành độ ${x_1}$, ${x_2}$ của các giao điểm.
2. Điều kiện để phương trình bậc hai có hai nghiệm phân biệt:
Để đường thẳng cắt parabol tại hai điểm phân biệt, phương trình hoành độ giao điểm (*) phải có hai nghiệm thực phân biệt. Điều này xảy ra khi biệt thức Delta của phương trình đó lớn hơn không ($\Delta > 0$). Biệt thức $\Delta$ được tính bằng công thức $\Delta = b^2 - 4ac$.
3. Định lý Viète:
Khi phương trình bậc hai (*) có hai nghiệm phân biệt ${x_1}$ và ${x_2}$, định lý Viète phát biểu rằng ${x_1} + {x_2} = -\frac{b}{a}$ và ${x_1}{x_2} = \frac{c}{a}$.

Các bài tập cùng chuyên đề
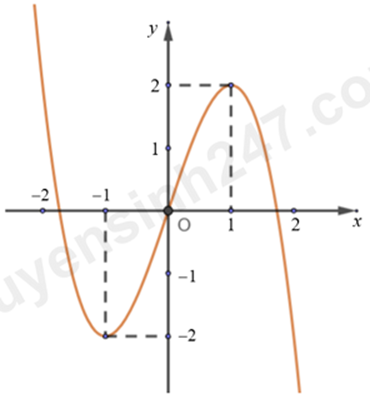
Cho hàm số bậc ba \(f\left( x \right)\) có đồ thị như hình vẽ. Số nghiệm thực của phương trình \({f^2}\left( x \right) - 3f\left( x \right) = - 2\) là:
-
A.
3
-
B.
4
-
C.
5
-
D.
6
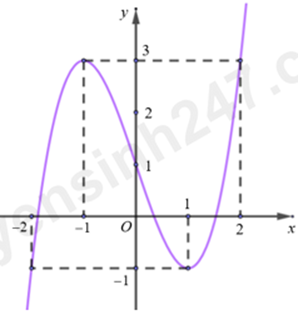
Cho hàm số bậc ba \(f(x)\) có đồ thị như hình vẽ. Hỏi có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left[ {f\left( x \right)} \right] = m\) có đúng \(4\) nghiệm phân biệt thuộc đoạn \(\left[ { - 1;2} \right]\)?
-
A.
1
-
B.
2
-
C.
3
-
D.
4
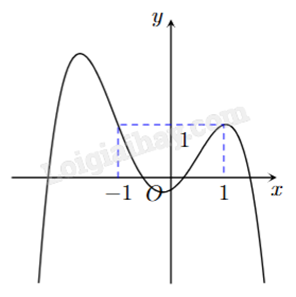
Cho hàm số đa thức bậc bốn y = f(x) có đồ thị như hình vẽ bên. Phương trình f(x) − 1 = 0 có bao nhiêu nghiệm thực phân biệt?
-
A.
3
-
B.
1
-
C.
2
-
D.
4
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số \(y = 2{x^3} - 3{x^2} + 2\) cắt đồ thị hàm số \(y = {x^3} - 6{x^2} + 9x + m\) tại 3 điểm phân biệt?







Danh sách bình luận