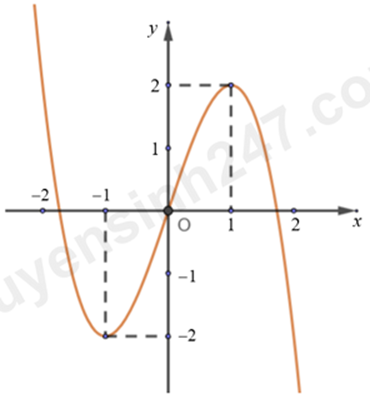
Cho hàm số bậc ba \(f\left( x \right)\) có đồ thị như hình vẽ. Số nghiệm thực của phương trình \({f^2}\left( x \right) - 3f\left( x \right) = - 2\) là:
-
A.
3
-
B.
4
-
C.
5
-
D.
6
Sử dụng tương giao đồ thị.
Ta có: \({f^2}\left( x \right) - 3f\left( x \right) = - 2 \Leftrightarrow {f^2}\left( x \right) - 3f\left( x \right) + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 1\\f\left( x \right) = 2\end{array} \right..\)
Nhìn hình vẽ ta thấy:
Đồ thị hàm số \(y = f\left( x \right)\) cắt đường thẳng \(y = 1\) tại 3 điểm \( \Rightarrow \) Phương trình \(f\left( x \right) = 1\) có 3 nghiệm.
Đồ thị hàm số \(y = f\left( x \right)\) cắt đường thẳng \(y = 2\) tại 2 điểm \( \Rightarrow \) Phương trình \(f\left( x \right) = 1\) có 2 nghiệm.
Vậy phương trình đã cho có tất cả 5 nghiệm.
Đáp án : C
Các bài tập cùng chuyên đề
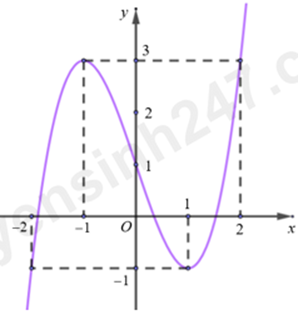
Cho hàm số bậc ba \(f(x)\) có đồ thị như hình vẽ. Hỏi có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left[ {f\left( x \right)} \right] = m\) có đúng \(4\) nghiệm phân biệt thuộc đoạn \(\left[ { - 1;2} \right]\)?
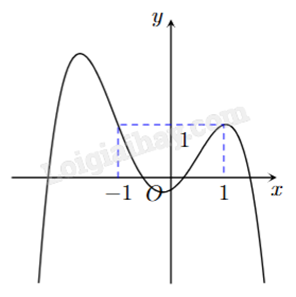
Cho hàm số đa thức bậc bốn y = f(x) có đồ thị như hình vẽ bên. Phương trình f(x) − 1 = 0 có bao nhiêu nghiệm thực phân biệt?
