Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Chứng minh AH là đường trung trực của BC.
- Chứng minh: \(\Delta ABM = \Delta ACM\) suy ra MB = MC.
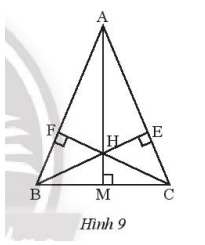
Ta có AH là đường cao vuông góc với cạnh BC tại M.
Xét hai tam giác vuông ABM và ACM có:
Cạnh huyền bằng nhau: AB = AC
Cạnh góc vuông AM chung
Suy ra: \(\Delta ABM = \Delta ACM\) (cạnh huyền – cạnh góc vuông)
Suy ra MB = MC
Vậy AH là đường trung trực của BC

Các bài tập cùng chuyên đề
Mỗi tam giác có mấy đường trung trực
Cho tam giác ABC, em hãy dùng thước kẻ và compa vẽ đường trung trực xy của cạnh BC.
Ở Hình 1, cho biết AE = AF và \(\widehat {ABC} = \widehat {ACB}\). Chứng minh AH là đường trung trực của BC.
Hình 121 minh họa biển giới thiệu quần thể di tích, danh thắng cấp Quốc gia núi Dũng Quyết và khu vực Phượng Hoàng Trung Đô ở tỉnh Nghệ An (Hình 120).

Làm thế nào để xác định được vị trí cách đều ba địa điểm được minh họa trong Hình 121?
Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung trực của tam giác ABC.
Cho C là trung điểm của đoạn thẳng AB. Gọi Ax, By là hai đường thẳng vuông góc với AB tại A và tại B. Một đường thẳng qua C cắt Ax tại M, cắt By tại P. Điểm N nằm trên tia đối của tia BP sao cho góc MCN là góc vuông. Gọi H là hình chiếu của C trên MN.
Chứng minh:
a) AM + BN = MN;
b) CM là đường trung trực của AH, CN là đường trung trực của BH;
c) Góc AHB là góc vuông.
Cho tam giác ABC có góc A bằng \({120^o}\). Các đường trung trực của AB và Ac lần lượt cắt Bc tại M và N. Tính số đo góc MAN.
Cho tam giác ABC có đường trung trực cạnh AC đi qua đỉnh B, chứng minh tam giác ABC là tam giác cân







Danh sách bình luận