Cho điểm \(M\left( {4;5} \right)\). Tìm tọa độ:
a) Điểm H là hình chiếu vuông góc của điểm M trên trục \(Ox\).
b) Điểm M’ đối xứng với M qua trục \(Ox\).
c) Điểm K là hình chiếu vuông góc của điểm M trên trục \(Oy\).
d) Điểm M’’ đối xứng với M qua trục \(Oy\).
e) Điểm C đối xứng với M qua gốc O.
+ Cho hai vectơ \(\overrightarrow a = \left( {{a_1},{a_2}} \right),\overrightarrow b = \left( {{b_1},{b_2}} \right)\), ta có: \(\overrightarrow a \bot \overrightarrow b \Rightarrow {a_1}.{b_1} + {a_2}.{b_2} = 0\).
+ Cho hai điểm \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\). Tọa độ trung điểm \(M\left( {{x_M},{y_M}} \right)\) của đoạn thẳng AB là: \({x_M} = \frac{{{x_A} + {x_B}}}{2};{y_M} = \frac{{{y_A} + {y_B}}}{2}\).
a)
+ \(MH \bot Ox = H \Rightarrow H \in Ox \Rightarrow H\left( {a;0} \right)\).
+ \(\overrightarrow {MH} = \left( {a - 4; - 5} \right),\overrightarrow {{v_{Ox}}} = \left( {1;0} \right) \Rightarrow a - 4 + 0 = 0 \Rightarrow a = 4 \Rightarrow H\left( {4;0} \right)\).
b) Điểm M’ đối xứng với M qua trục \(Ox\) \( \Rightarrow \) H là trung điểm của MM’ \( \Rightarrow \) \(M'\left( {4; - 5} \right)\).
c)
+ \(MH \bot Oy = H \Rightarrow K \in Oy \Rightarrow H\left( {0;b} \right)\).
+ \(\overrightarrow {MK} = \left( { - 4;b - 5} \right),\overrightarrow {{v_{Ox}}} = \left( {0;1} \right) \Rightarrow 0 + b - 5 = 0 \Rightarrow b = 5 \Rightarrow K\left( {0;5} \right)\).
d) Điểm M’’ đối xứng với M qua trục \(Oy\)\( \Rightarrow \) K là trung điểm của MM’’ \( \Rightarrow \) \(M''\left( { - 4;5} \right)\).
e) Điểm C đối xứng với M qua gốc O \( \Rightarrow \) O là trung điểm của CM \( \Rightarrow \) \(C\left( { - 4; - 5} \right)\).

Các bài tập cùng chuyên đề
Hãy tìm cách xác định vị trí các quân mã trên bàn cờ vua.

Cho bốn điểm \(A(3;5),B(4;0),C(0; - 3),D(2;2)\). Trong các điểm đã cho, hãy tìm điểm:
a) Thuộc trục hoành.
b) Thuộc trục tung.
c) Thuộc đường phân giác của góc phần tư thứ nhất.
Cho điểm \(M\left( {{x_0};{y_0}} \right)\). Tìm tọa độ:
a) Điểm H là hình chiếu vuông góc của M trên trục Ox.
b) Điểm M’ đối xứng với M qua trục Ox.
c) Điểm K là hình chiếu vuông góc của M trên trục Oy.
d) Điểm M’’ đối xứng với M qua trục Oy.
e) Điểm C đối xứng với M qua gốc tọa độ.
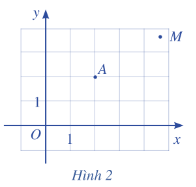
Trong mặt phẳng toạ độ Oxy (Hình 2), hãy:
a) Tìm hoành độ và tung độ của điểm A.
b) Nêu cách xác định toạ độ của điểm M tuỳ ý.
Cho điểm M trong mặt phẳng toạ độ Oxy.
a) Vẽ vecto \(\overrightarrow {OM} \).
b) Nêu cách xác định toạ độ của điểm M.
Trong mặt phẳng toạ độ Oxy, cho điểm M(-1; 3).
a) Tìm toạ độ điểm A đối xứng với điểm M qua gốc O.
b) Tìm toạ độ điểm B đối xứng với điểm M qua trục Ox.
c) Tìm toạ độ điểm C đối xứng với điểm M qua trục Oy.
Cho năm điểm \(A\left( {2;0} \right),B\left( {0; - 2} \right),C\left( {3;3} \right),D\left( { - 2; - 2} \right),E\left( {1; - 1} \right)\). Trong các điểm đã cho, hãy tìm điểm:
a) Thuộc trục hoành.
b) Thuộc trục tung.
c) Thuộc đường phân giác của góc phần tư thứ nhất.







Danh sách bình luận