Cho bốn điểm \(A(3;5),B(4;0),C(0; - 3),D(2;2)\). Trong các điểm đã cho, hãy tìm điểm:
a) Thuộc trục hoành.
b) Thuộc trục tung.
c) Thuộc đường phân giác của góc phần tư thứ nhất.
a) Điểm thuộc trục hoành có tung độ bằng 0.
b) Điểm thuộc trục tung có hoành độ bằng 0.
c) Điểm thuộc góc phần tư thứ nhất có tung độ bằng hoành độ.
a) Vì điểm thuộc hoành độ có tung độ bằng 0 nên ta có điểm B thuộc trục hoành.
b) Vì điểm thuộc tung độ có hoành độ bằng 0 nên ta có điểm C thuộc trục tung.
c) Vì điểm thuộc góc phần tư thứ nhất có tung độ bằng hoành độ nên ta có điểm thuộc đường phân giác góc phần tư thứ nhất là điểm D.
Các bài tập cùng chuyên đề
Hãy tìm cách xác định vị trí các quân mã trên bàn cờ vua.
Cho điểm \(M\left( {{x_0};{y_0}} \right)\). Tìm tọa độ:
a) Điểm H là hình chiếu vuông góc của M trên trục Ox.
b) Điểm M’ đối xứng với M qua trục Ox.
c) Điểm K là hình chiếu vuông góc của M trên trục Oy.
d) Điểm M’’ đối xứng với M qua trục Oy.
e) Điểm C đối xứng với M qua gốc tọa độ.
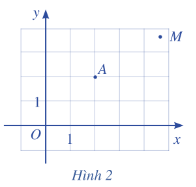
Trong mặt phẳng toạ độ Oxy (Hình 2), hãy:
a) Tìm hoành độ và tung độ của điểm A.
b) Nêu cách xác định toạ độ của điểm M tuỳ ý.
Cho điểm M trong mặt phẳng toạ độ Oxy.
a) Vẽ vecto \(\overrightarrow {OM} \).
b) Nêu cách xác định toạ độ của điểm M.
Trong mặt phẳng toạ độ Oxy, cho điểm M(-1; 3).
a) Tìm toạ độ điểm A đối xứng với điểm M qua gốc O.
b) Tìm toạ độ điểm B đối xứng với điểm M qua trục Ox.
c) Tìm toạ độ điểm C đối xứng với điểm M qua trục Oy.
Cho năm điểm \(A\left( {2;0} \right),B\left( {0; - 2} \right),C\left( {3;3} \right),D\left( { - 2; - 2} \right),E\left( {1; - 1} \right)\). Trong các điểm đã cho, hãy tìm điểm:
a) Thuộc trục hoành.
b) Thuộc trục tung.
c) Thuộc đường phân giác của góc phần tư thứ nhất.
Cho điểm \(M\left( {4;5} \right)\). Tìm tọa độ:
a) Điểm H là hình chiếu vuông góc của điểm M trên trục \(Ox\).
b) Điểm M’ đối xứng với M qua trục \(Ox\).
c) Điểm K là hình chiếu vuông góc của điểm M trên trục \(Oy\).
d) Điểm M’’ đối xứng với M qua trục \(Oy\).
e) Điểm C đối xứng với M qua gốc O.
Trong tiết học thực hành môn Giáo dục quốc phòng, thầy giáo gọi 1 học sinh lên sân tập mẫu một số động tác cơ bản. Biết từ vị trí xuất phát thầy yêu cầu bạn này bước lên phía trước 2 bước rồi bước sang phải 3 bước thì dừng lại. Nếu coi vị trí ban đầu của bạn học sinh này là gốc tọa độ trong mặt phẳng tọa độ Oxy và từ vị trí ban đầu hướng sang phải là tia Ox, hướng lên phía trước là tia Oy và mỗi bước di chuyển của bạn này là 1 đơn vị độ dài thì khi dừng lại bạn này ở vị trí M(a; b). Tính 2a - b.
Danh sách bình luận