Cho nửa đường tròn tâm I bán kính r quay quanh đường kính AB cố định của nó, ta nhận được một mặt cầu (S) tâm I bán kính r. Xét một điểm M thuộc (S) (Hình 5.32). Hãy so sánh IM và r.
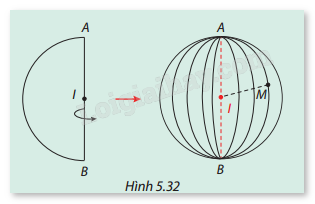
Khoảng cách từ tâm nửa đường tròn tới bất kỳ điểm nào nằm trên nửa đường tròn đều bằng nhau.
Vì M là vị trí của một điểm thuộc nửa đường tròn quay quanh AB, nên điểm M luôn có cùng khoảng cách từ I đến điểm đó như khoảng cách từ I đến bất kỳ điểm nào trên nửa đường tròn ban đầu, tức là IM = r.
Do bán kính không thay đổi trong suốt quá trình quay, khoảng cách từ I đến M vẫn giữ nguyên giá trị là 𝑟.

Các bài tập cùng chuyên đề
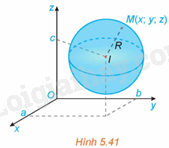
Trong không gian Oxyz, cho mặt cầu (S) tâm và bán kính R (H.5.41). Khi đó, một điểm thuộc mặt cầu (S) khi và chỉ khi nó thỏa mãn điều kiện gì?
Tính khoảng cách trên mặt đất từ vị trí A là giao giữa kinh tuyến gốc với xích đạo đến vị trí B: \({45^o}N,{30^o}E\).
Trong không gian Oxyz, một thiết bị phát sóng đặt tại vị trí \(A\left( {2;0;0} \right).\) Vùng phủ sóng của thiết bị có bán kính bằng 1. Hỏi vị trí \(M\left( {2;1;1} \right)\) có thuộc vùng phủ sóng của thiết bị nói trên hay không?
Nếu quay đường tròn tâm I bán kính R quanh đường kính AB một vòng (Hình 39) thì hình tạo thành được gọi là mặt cầu. Những điểm thuộc mặt cầu đó cách I một khoảng bằng bao nhiêu?
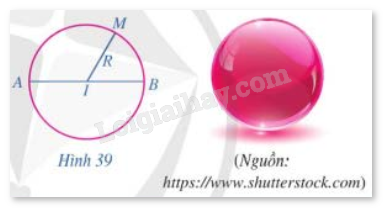
Cho hai điểm M(x; y; z) và I(a; b; c).
a) Viết công thức tính khoảng cách giữa hai điểm M và I.
b) Nêu mối liên hệ giữa x, y và z để M nằm trên mặt cầu tâm I bán kính R.







Danh sách bình luận