Tính khoảng cách trên mặt đất từ vị trí A là giao giữa kinh tuyến gốc với xích đạo đến vị trí B: \({45^o}N,{30^o}E\).
Sử dụng kiến thức về xác định tọa độ của các điểm trên bề mặt Trái Đất để tính: Nếu vị trí P có vĩ độ, kinh độ tương ứng là \({\alpha ^o}N,{\beta ^o}E\left( {0 < \alpha < 90,0 < \beta < 180} \right)\) thì tọa độ của P là \(P\left( {\cos {\alpha ^o}\cos {\beta ^o},\cos {\alpha ^o}\sin {\beta ^o},\sin {\alpha ^o}} \right)\).
Vì A là giao giữa kinh tuyến gốc với xích đạo nên \(A\left( {1;0;0} \right)\), do đó \(\overrightarrow {OA} \left( {1;0;0} \right)\).
Ta có: \(B\left( {\cos {{45}^o}\cos {{30}^o},\cos {{45}^o}\sin {{30}^o},\sin {{45}^o}} \right)\) nên \(\overrightarrow {OB} \left( {\frac{{\sqrt 6 }}{4};\frac{{\sqrt 2 }}{4};\frac{{\sqrt 2 }}{2}} \right)\), \(\overrightarrow {OA} .\overrightarrow {OB} = \frac{{\sqrt 6 }}{4}\)
Vì A, B thuộc mặt đất nên \(\left| {\overrightarrow {OA} } \right| = \left| {\overrightarrow {OB} } \right| = 1\)
Do đó, \(\cos \widehat {AOB} = \frac{{\overrightarrow {OA} .\overrightarrow {OB} }}{{\left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|}} = \frac{{\sqrt 6 }}{4} \Rightarrow \widehat {AOB} \approx 52,{2388^o}\)
Mặt khác, đường tròn tâm O, đi qua A, B bán kính 1 và chu vi là \(2\pi \approx 6,2832\) nên cung nhỏ AB của đường tròn có độ dài xấp xỉ bằng \(\frac{{52,2388}}{{360}}.6,2832 \approx 0,9117\)
Do 1 đơn vị độ dài trong không gian Oxyz tương ứng với 6 371km trên thực tế, nên khoảng cách giữa hai vị trí A, B xấp xỉ bằng \(0,9117.6\;371 = 5\;808,4407\left( {km} \right)\)

Các bài tập cùng chuyên đề
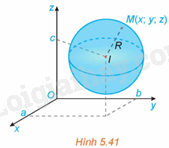
Trong không gian Oxyz, cho mặt cầu (S) tâm và bán kính R (H.5.41). Khi đó, một điểm thuộc mặt cầu (S) khi và chỉ khi nó thỏa mãn điều kiện gì?
Trong không gian Oxyz, một thiết bị phát sóng đặt tại vị trí \(A\left( {2;0;0} \right).\) Vùng phủ sóng của thiết bị có bán kính bằng 1. Hỏi vị trí \(M\left( {2;1;1} \right)\) có thuộc vùng phủ sóng của thiết bị nói trên hay không?
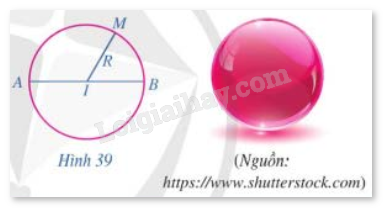
Nếu quay đường tròn tâm I bán kính R quanh đường kính AB một vòng (Hình 39) thì hình tạo thành được gọi là mặt cầu. Những điểm thuộc mặt cầu đó cách I một khoảng bằng bao nhiêu?
Cho hai điểm M(x; y; z) và I(a; b; c).
a) Viết công thức tính khoảng cách giữa hai điểm M và I.
b) Nêu mối liên hệ giữa x, y và z để M nằm trên mặt cầu tâm I bán kính R.
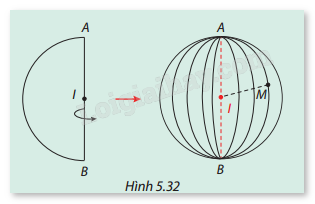
Cho nửa đường tròn tâm I bán kính r quay quanh đường kính AB cố định của nó, ta nhận được một mặt cầu (S) tâm I bán kính r. Xét một điểm M thuộc (S) (Hình 5.32). Hãy so sánh IM và r.







Danh sách bình luận