Cho hai điểm M(x; y; z) và I(a; b; c).
a) Viết công thức tính khoảng cách giữa hai điểm M và I.
b) Nêu mối liên hệ giữa x, y và z để M nằm trên mặt cầu tâm I bán kính R.
a) Sử dụng công thức tính khoảng cách về hai điểm trong không gian để tính: Cho điểm \(A\left( {{a_1};{a_2};{a_3}} \right)\) và \(B\left( {{b_1};{b_2};{b_3}} \right)\). Khi đó, \(AB = \sqrt {{{\left( {{b_1} - {a_1}} \right)}^2} + {{\left( {{b_2} - {a_2}} \right)}^2} + {{\left( {{b_3} - {a_3}} \right)}^2}} \).
b) Sử dụng kiến thức về vị trí của điểm so với mặt cầu để tìm bán kính của mặt cầu: Cho mặt cầu tâm I, bán kính R và điểm M bất kì trong không gian. Điểm M thuộc mặt cầu tâm I, bán kính R khi và chỉ khi \(IM = R\).
a) Công thức tính khoảng cách giữa hai điểm M và I là: \(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} \).
b) Để M nằm trên mặt cầu tâm I bán kính R thì \(IM = R\) hay \(\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} = R\).

Các bài tập cùng chuyên đề
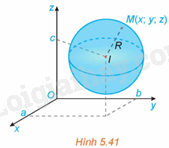
Trong không gian Oxyz, cho mặt cầu (S) tâm và bán kính R (H.5.41). Khi đó, một điểm thuộc mặt cầu (S) khi và chỉ khi nó thỏa mãn điều kiện gì?
Tính khoảng cách trên mặt đất từ vị trí A là giao giữa kinh tuyến gốc với xích đạo đến vị trí B: \({45^o}N,{30^o}E\).
Trong không gian Oxyz, một thiết bị phát sóng đặt tại vị trí \(A\left( {2;0;0} \right).\) Vùng phủ sóng của thiết bị có bán kính bằng 1. Hỏi vị trí \(M\left( {2;1;1} \right)\) có thuộc vùng phủ sóng của thiết bị nói trên hay không?
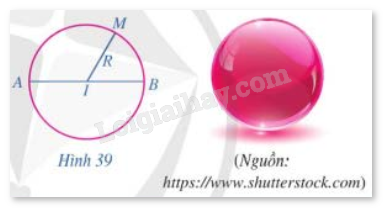
Nếu quay đường tròn tâm I bán kính R quanh đường kính AB một vòng (Hình 39) thì hình tạo thành được gọi là mặt cầu. Những điểm thuộc mặt cầu đó cách I một khoảng bằng bao nhiêu?
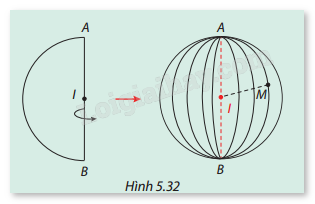
Cho nửa đường tròn tâm I bán kính r quay quanh đường kính AB cố định của nó, ta nhận được một mặt cầu (S) tâm I bán kính r. Xét một điểm M thuộc (S) (Hình 5.32). Hãy so sánh IM và r.







Danh sách bình luận