Cho tam giác \(MNP\) có \(H \in MN,\,K \in MP\). Điều kiện không kết luận được \(HK\parallel NP\) là:
-
A.
\(\frac{{MH}}{{MN}} = \frac{{MK}}{{MP}}\)
-
B.
\(\frac{{MH}}{{HN}} = \frac{{MK}}{{KP}}\)
-
C.
\(\frac{{NH}}{{MN}} = \frac{{MP}}{{KP}}\)
-
D.
\(\frac{{NH}}{{MN}} = \frac{{PK}}{{MP}}\)
Định lý Thales đảo được phát biểu như sau: Nếu một đường thẳng cắt hai cạnh của tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỷ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Có \(\frac{{NH}}{{MN}}\) và \(\frac{{MP}}{{KP}}\) không tương ứng tỉ lệ nên \(HK\) không song song với \(PN\).
Đáp án : C

Các bài tập cùng chuyên đề
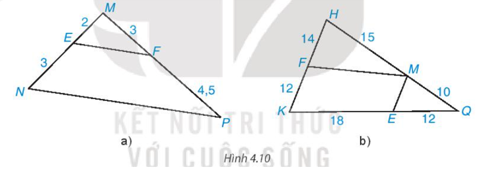
Tìm các cặp đường thẳng song song trong Hình 4.10 và giải thích tại sao chúng song song với nhau.
Cho tam giác ABC, điểm I thuộc cạnh AB, điểm K thuộc cạnh AC. Kẻ IM song song với BK (M thuộc AC), kẻ KN song song với CI (N thuộc AB). Chứng minh MN song song với BC.
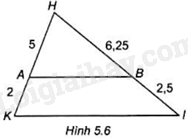
Cho Hình 5.6. Chứng minh rằng AB//KI
Tìm các cặp đường thẳng song song trong Hình 4.5 và giải thích vì sao chúng song song với nhau.

Hãy chỉ ra các cặp đường thẳng song song với nhau trong mỗi hình dưới đây.

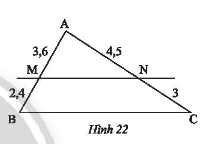
Quan sát Hình 22, chứng minh rằng \(MN//BC\).
Quan sát Hình 24, chỉ ra các cặp đường thẳng song song và chứng minh điều ấy.

Cho tam giác ABC vuông tại A có CA = 4, CB = 5. Giả sử M, N là hai điểm lần lượt nằm trên hai cạnh CA, CB sao cho CM = 1, CN = 1,25. Tính độ dài đoạn thẳng MN.
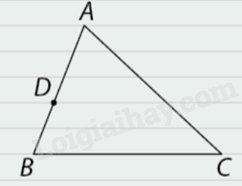
Trong Hình 6.11, tam giác \(ABC\) được vẽ trên giấy vở học sinh.
1. Tính tỉ số \(\frac{{AD}}{{BD}}.\)
2. Xác định điểm \(E\) trên cạnh \(AC\) sao cho \(\frac{{DA}}{{DB}} = \frac{{EA}}{{EC}}.\) Có bao nhiêu điểm như vậy?
3. Theo em, \(DE\) có song somg với \(BC\) không?
Trong Hình 6.14, đường thẳng \(DE\) và \(FG\) có song song với \(AC\) không? Vì sao?

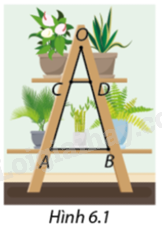
Quay lại bài toán khởi động (hình 6.1): Chỉ dùng thước đo độ dài, làm cách nào để có thể xác định được các cạnh \(AB\) và \(CD\) của hai mặt kệ có song song với nhau không?
Em hãy giải thích bằng cách nào bác thợ mộc có thể xác định được cạnh của hai tầng kệ chữ \(A\) song song với nhau mà chỉ dùng thước đo độ dài.
Viết tên các đường thẳng song song trong Hình 6.16.

Cho hình vẽ. Chọn đáp án đúng trong các đáp án sau.
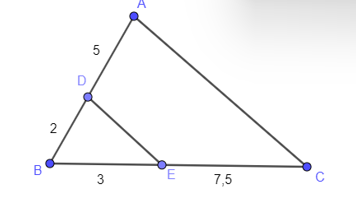
-
A.
\(AD\parallel EC\);
-
B.
\(DE\parallel AC\);
-
C.
\(DE\parallel BC\);
-
D.
\(BE\parallel AC\).
Cho tam giác \(ABC\) có điểm \(M\) trên cạnh \(BC\) sao cho \(BC = 4CM\). Trên cạnh \(AC\) lấy điểm \(N\) sao cho \(\frac{{CN}}{{AN}} = \frac{1}{3}\). Khẳng định nào sau đây là đúng khi nói về mối quan hệ giữa hai đường thẳng \(AB\) và \(MN\).
-
A.
\(AB\parallel MN\);
-
B.
\(AB \bot MN\);
-
C.
\(AB\) cắt \(MN\);
-
D.
Cả B và C đều đúng.
Cho hình vẽ dưới, khẳng định nào sau đây là đúng?
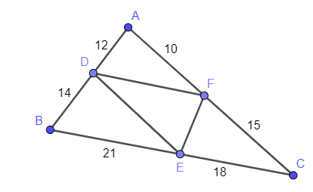
-
A.
\(EF\parallel AD\);
-
B.
\(DF\parallel BC\);
-
C.
\(EF\parallel AB\)
-
D.
\(DE\parallel AC\)
Cho tứ giác \(MNPQ\), gọi \(K,\, L\) lần lượt là trọng tâm của tam giác \(MNP\) và \(NPQ\). Khi đó \(KL\) song song với đường thẳng nào dưới đây?
-
A.
\(MP\);
-
B.
\(NM\);
-
C.
\(NQ\);
-
D.
\(MQ\).
Cho hình bên, biết \(AB = 9\,cm\), \(AC = 12\,cm\), \(IB = 6,cm\), \(KC = 8\,cm\). Kết luận nào sau đây là đúng?
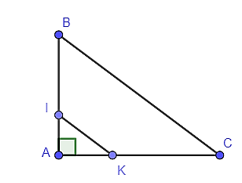
-
A.
\(IK \bot BC\);
-
B.
\(IK\parallel BC\);
-
C.
\(IK = BC\);
-
D.
Cả A, B, C đều sai.
Cho tam giác \(ABC\) có ba góc nhọn, đường cao \(AH\). Trên \(AH,AB,AC\) lần lượt lấy các điểm \(D,E,F\) sao cho \(\widehat {EDC} = \widehat {FDB} = 90^\circ \). Chứng minh: \(EF//BC\).
Hãy chọn câu sai. Cho hình vẽ với $AB<AC$:
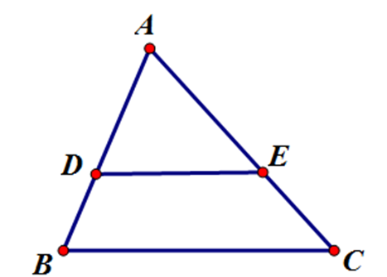
-
A.
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} \Rightarrow DE//BC\).
-
B.
\(\dfrac{{AD}}{{DB}} = \dfrac{{AE}}{{EC}} \Rightarrow DE//BC\).
-
C.
\(\dfrac{{AB}}{{DB}} = \dfrac{{AC}}{{EC}} \Rightarrow DE//BC\).
-
D.
\(\dfrac{{AD}}{{DE}} = \dfrac{{AE}}{{ED}} \Rightarrow DE//BC\).
Cho hình vẽ. Điều kiện nào sau đây không suy ra được \(DE//BC\)?

-
A.
\(\dfrac{{DB}}{{DA}} = \dfrac{{EC}}{{EA}}\).
-
B.
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\).
-
C.
\(\dfrac{{AB}}{{DB}} = \dfrac{{AC}}{{EC}}\).
-
D.
\(\dfrac{{AD}}{{DE}} = \dfrac{{AE}}{{AC}}\).







Danh sách bình luận