Bạn Loan đặt một cái que lên bàn cờ vua như ở Hình 20. Bạn ấy nói rằng: Không sử dụng thước đo, có thể chia cái que đó thành ba phần bằng nhau. Em hãy giải thích tại sao?

Lấy thêm điểm và sử dụng định lý Thales để chia đoạn thẳng thành ba phần bằng nhau.
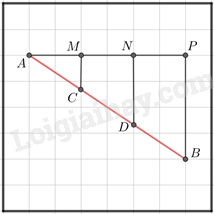
Đoạn thẳng AB biểu diễn cho cái que.
Trên bàn cờ lấy một điểm P nằm ngoài đoạn thẳng AB sao cho AP có độ dài 6 ô vuông.
Nối AP, BP.
Trên đoạn thẳng AP lấy hai điểm M và N sao cho AM = MN = NP = 2 ô vuông.
Tại M, N kẻ các đường thẳng vuông góc với AP và cắt AB lần lượt tại C và D.
=> MC // ND // PB
Áp dụng định lý Thales trong tam giác APB thì \(\frac{AM}{AP} = \frac{AC}{AB} = \frac{1}{3} \Rightarrow AC = \frac{1}{3}AB\) và \(\frac{AN}{AP} = \frac{AD}{AB} = \frac{2}{3}\Rightarrow AD = \frac{2}{3}AB\).
Khi đó AC = CD = DB = \(\frac{1}{3}\)AB.
Vậy ta đã chia cái que thành 3 phần bằng nhau mà không cần dùng thước đo.

Các bài tập cùng chuyên đề
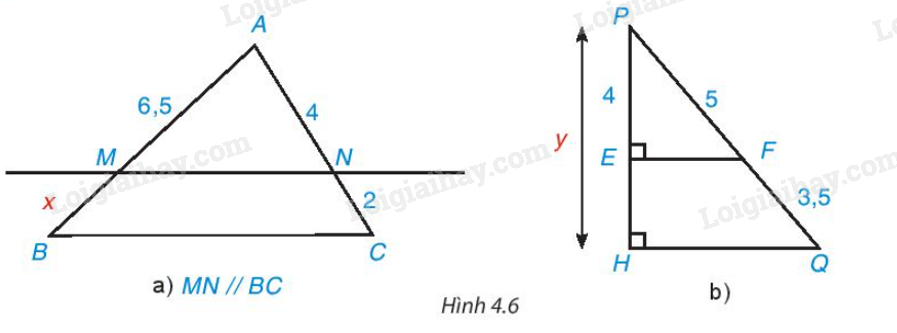
Tìm các độ dài x, y trong Hình 4.6.
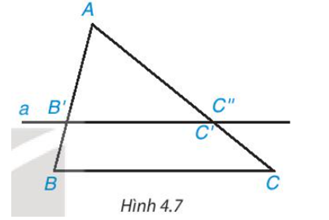
Cho ∆ABC có AB = 6 cm, AC = 9 cm. Trên cạnh AB lấy điểm B’, trên cạnh AC lấy điểm C’ sao cho AB’ = 4 cm, AC’ = 6 cm (H.4.7).
• So sánh các tỉ số \(\dfrac{{AB'}}{{AB}}\) và \(\dfrac{{AC'}}{{AC}}\)
• Vẽ đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’. Tính độ dài đoạn thẳng AC’’.
• Nhận xét gì về hai điểm C’, C’’ và hai đường thẳng B’C’, BC?
Cây cầu AB bắc qua một con sông có chiều rộng 300 m. Để đo khoảng cách giữa hai điểm C và D trên hai bờ con sông, người ta chọn một điểm E trên đường thẳng AB sao cho ba điểm E, C, D thẳng hàng. Trên mặt đất, người ta đo được AE = 400 m, EC = 500 m. Theo em, người ta tính khoảng cách giữa C và D như thế nào?
Tìm độ dài x, y trong Hình 4.9 (làm tròn kết quả đến chữ số thập phân thứ nhất).
Cho ∆ABC, từ điểm D trên cạnh BC, kẻ đường thẳng song song với AB cắt AC tại F và kẻ đường thẳng song song với AC cắt AB tại E.
Chứng minh rằng: \(\dfrac{{A{\rm{E}}}}{{AB}} + \dfrac{{AF}}{{AC}} = 1\)
Cho ∆ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB, d cắt BC tại điểm M. Chứng minh rằng \(BM = \dfrac{1}{3}BC\)
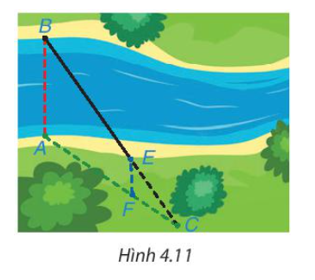
Để đo khoảng cách giữa hai vị trí B và E ở hai bên bờ sông, bác An chọn ba vị trí A, F, C cùng nằm ở một bên bờ sông sao cho ba điểm C, E, B thẳng hàng, ba điểm C, F, A thẳng hàng và AB // EF (H.4.11). Sau đó bác An đo được AF = 40 m, FC = 20 m, EC = 30 m. Hỏi khoảng cách giữa hai vị trí B và E bằng bao nhiêu?
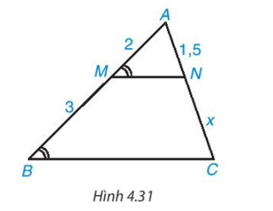
Độ dài x trong Hình 4.31 bằng
A. 2,75
B. 2.
C. 2,25.
D. 3,75.
Cho tam giác ABC có AB = 9 cm, D là điểm thuộc cạnh AB sao cho AD = 6 cm. Kẻ DE song song với BC (E thuộc AC), kẻ EF song song với CD (F thuộc AB). Độ dài AF bằng
A. 4 cm.
B. 5 cm.
C. 6 cm.
D. 7 cm.
Cho góc xOy. Trên tia Ox, lấy hai điểm A và B sao cho OA = 2 cm, OB = 5 cm. Trên tia Oy, lấy điểm C sao cho OC = 3 cm. Từ điểm B kẻ đường thẳng song song với AC cắt Oy tại D. Tính độ dài đoạn thẳng CD.
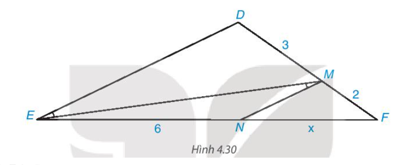
Tìm độ dài x trong Hình 4.30
Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K. Chứng minh rằng: \(D{M^2}\) = MN . MK.
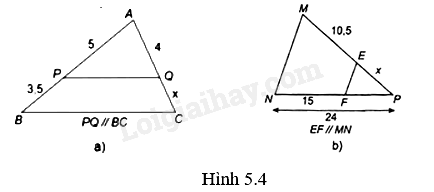
Tìm độ dài x trong các hình vẽ sau (H.5.4)
Tìm độ dài x trong Hình 5.5:

Cho hình thang ABCD (AB//DC). Một đường thẳng song song với hai đáy cắt các đoạn thẳng AD, AC, BC theo thứ tự tại M, I, N. Chứng minh rằng:
a) \(\frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}\);
b) \(\frac{{AM}}{{AD}} + \frac{{CN}}{{CB}} = 1\).
Độ dài x trong Hình 5.13 là

A. 20
B. 50
C. 12
D. 30
Cho hình thang ABCD (AB//DC). Gọi O là giao điểm của AC và BD. Xét các khẳng định sau:
(1) \(\frac{{OA}}{{OC}} = \frac{{OD}}{{OB}}\)
(2) \(OA.OD = OB.OC\)
(3) \(\frac{{AO}}{{AC}} = \frac{{BO}}{{BD}}\)
Số khẳng định đúng là:
A. 0
B. 1
C. 2
D. 3
Cho Hình 5.14, biết DE//AC. Độ dài x là
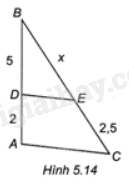
A. 5
B. 7
C. 6,5
D. 6,25
Cho Hình 5.15, biết \(ED \bot AB,AC \bot AB.\) Khi đó, x có giá trị là

A. 2,5
B. 2
C. 3
D. 4
Cho hình bình hành ABCD, điểm E thuộc cạnh AB (E khác A và B), điểm F thuộc cạnh AD (F khác A và D). Đường thẳng qua D song song với EF cắt AC tại I. Đường thẳng qua B song song với EF cắt AC tại K.
a) Chứng minh rằng \(AI = CK\).
b) Gọi N là giao điểm của EF và AC. Chứng minh rằng: \(\frac{{AB}}{{AE}} + \frac{{AD}}{{AF}} = \frac{{AC}}{{AN}}\).
Cho góc nhọn xOy. Trên cạnh Ox lấy điểm N, trên cạnh Oy lấy điểm M. Gọi I là một điểm trên đoạn thẳng MN. Qua I kẻ đường thẳng song song với Ox cắt Oy tại A (A khác M và N) và đường thẳng song song với Oy cắt Ox ở B. Chứng minh rằng \(\frac{{MA}}{{MO}} + \frac{{NB}}{{NO}} = 1\)
Quan sát Hình 4.1 biết MN // BC. Tỉ số \(\frac{{AM}}{{MB}}\) bằng
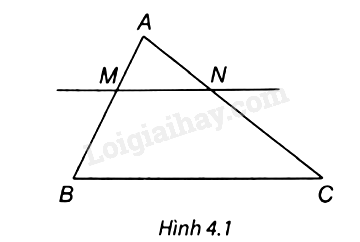
A. \(\frac{{AN}}{{AC}}\)
B. \(\frac{{AN}}{{NC}}\)
C. \(\frac{{NC}}{{AN}}\)
D. \(\frac{{BM}}{{AB}}\)
Quan sát Hình 4.2 và chọn khẳng định đúng.
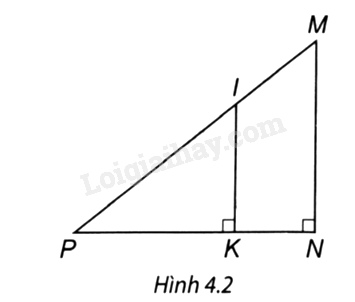
A. \(\frac{{PI}}{{PM}} = \frac{{KN}}{{PN}}.\)
B. \(\frac{{IM}}{{IP}} = \frac{{KP}}{{PN}}.\)
C. \(\frac{{MI}}{{MP}} = \frac{{NK}}{{NP}}.\)
D. \(\frac{{PI}}{{PM}} = \frac{{PK}}{{KN}}.\)
Quan sát Hình 4.3. Biết DE // BC, AD = 12, DB = 18, CE = 30. Độ dài AC bằng:

A. 20.
B. 56.
C. 45.
D. 50.
Tìm độ dài x, y trong Hình 4.4 (làm tròn kết quả đến chữ số thập phân thứ nhất).

Cho ∆ABC, từ điểm D trên cạnh BC, kẻ đường thẳng song song với AB cắt AC tại F và kẻ đường thẳng song song với AC cắt AB tại E. Chứng minh rằng: \(\frac{{AE}}{{AB}} + \frac{{AF}}{{AC}} = 1.\)
Cho ∆ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB, d cắt BC tại điểm M. Chứng minh rằng \(BM = \frac{1}{3}BC.\)
Để đo khoảng cách giữa hai vị trí B và E ở hai bên bờ sông, bác An chọn ba vị trí A, F, C cùng nằm ở một bên bờ sông sao cho ba điểm C, E, B thẳng hàng, ba điểm C, F, A thẳng hàng và AB // EF (H.4.8). Sau đó bác An đo được AF = 40 m, FC = 20 m, EC = 30 m. Hỏi khoảng cách giữa hai vị trí B và E bằng bao nhiêu?
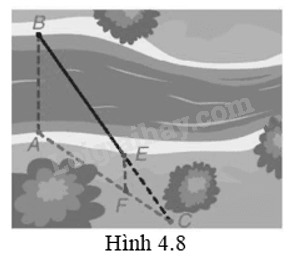
Cho hình thang ABCD (AB // DC), AC cắt BD tại I. Chứng minh rằng IA . ID = IB . IC.
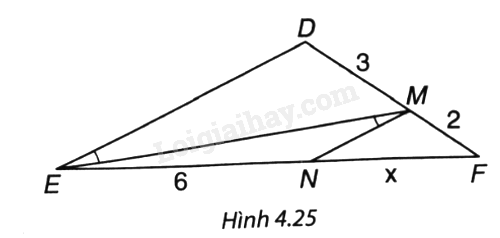
Tìm độ dài x trong Hình 4.25.









Danh sách bình luận