Cây cầu AB bắc qua một con sông có chiều rộng 300 m. Để đo khoảng cách giữa hai điểm C và D trên hai bờ con sông, người ta chọn một điểm E trên đường thẳng AB sao cho ba điểm E, C, D thẳng hàng. Trên mặt đất, người ta đo được AE = 400 m, EC = 500 m. Theo em, người ta tính khoảng cách giữa C và D như thế nào?
Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD, áp dụng định lí Thalès
Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD, áp dụng định lí Thalès, ta có:
\(\dfrac{{A{\rm{E}}}}{{AB}} = \dfrac{{CE}}{{C{\rm{D}}}}\) hay \(\dfrac{{400}}{{300}} = \dfrac{{500}}{{C{\rm{D}}}}\)
Suy ra \(C{\rm{D}} = \dfrac{{300.500}}{{400}} = 375\) (m).
Vậy khoảng cách giữa C và D bằng 375 m

Các bài tập cùng chuyên đề
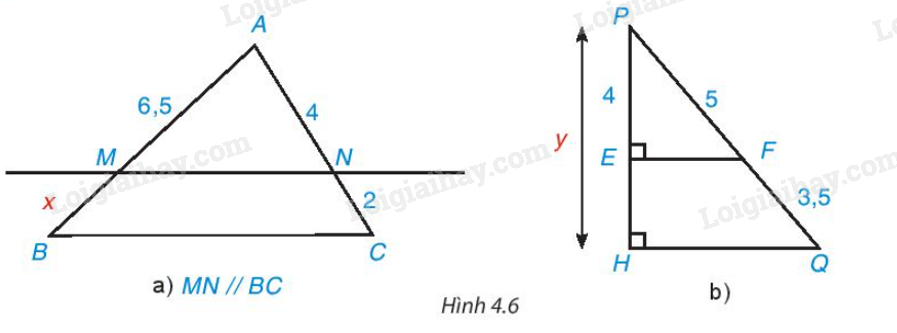
Tìm các độ dài x, y trong Hình 4.6.
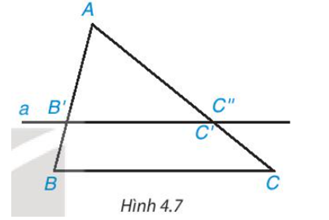
Cho ∆ABC có AB = 6 cm, AC = 9 cm. Trên cạnh AB lấy điểm B’, trên cạnh AC lấy điểm C’ sao cho AB’ = 4 cm, AC’ = 6 cm (H.4.7).
• So sánh các tỉ số \(\dfrac{{AB'}}{{AB}}\) và \(\dfrac{{AC'}}{{AC}}\)
• Vẽ đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’. Tính độ dài đoạn thẳng AC’’.
• Nhận xét gì về hai điểm C’, C’’ và hai đường thẳng B’C’, BC?
Tìm độ dài x, y trong Hình 4.9 (làm tròn kết quả đến chữ số thập phân thứ nhất).
Cho ∆ABC, từ điểm D trên cạnh BC, kẻ đường thẳng song song với AB cắt AC tại F và kẻ đường thẳng song song với AC cắt AB tại E.
Chứng minh rằng: \(\dfrac{{A{\rm{E}}}}{{AB}} + \dfrac{{AF}}{{AC}} = 1\)
Cho ∆ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB, d cắt BC tại điểm M. Chứng minh rằng \(BM = \dfrac{1}{3}BC\)
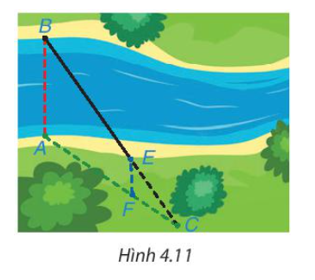
Để đo khoảng cách giữa hai vị trí B và E ở hai bên bờ sông, bác An chọn ba vị trí A, F, C cùng nằm ở một bên bờ sông sao cho ba điểm C, E, B thẳng hàng, ba điểm C, F, A thẳng hàng và AB // EF (H.4.11). Sau đó bác An đo được AF = 40 m, FC = 20 m, EC = 30 m. Hỏi khoảng cách giữa hai vị trí B và E bằng bao nhiêu?
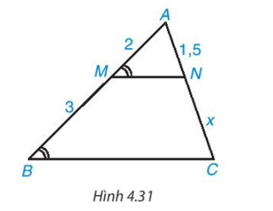
Độ dài x trong Hình 4.31 bằng
A. 2,75
B. 2.
C. 2,25.
D. 3,75.
Cho tam giác ABC có AB = 9 cm, D là điểm thuộc cạnh AB sao cho AD = 6 cm. Kẻ DE song song với BC (E thuộc AC), kẻ EF song song với CD (F thuộc AB). Độ dài AF bằng
A. 4 cm.
B. 5 cm.
C. 6 cm.
D. 7 cm.
Cho góc xOy. Trên tia Ox, lấy hai điểm A và B sao cho OA = 2 cm, OB = 5 cm. Trên tia Oy, lấy điểm C sao cho OC = 3 cm. Từ điểm B kẻ đường thẳng song song với AC cắt Oy tại D. Tính độ dài đoạn thẳng CD.
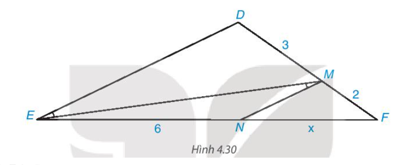
Tìm độ dài x trong Hình 4.30
Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K. Chứng minh rằng: \(D{M^2}\) = MN . MK.
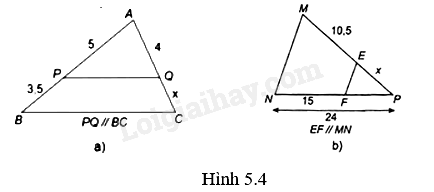
Tìm độ dài x trong các hình vẽ sau (H.5.4)
Tìm độ dài x trong Hình 5.5:

Cho hình thang ABCD (AB//DC). Một đường thẳng song song với hai đáy cắt các đoạn thẳng AD, AC, BC theo thứ tự tại M, I, N. Chứng minh rằng:
a) \(\frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}\);
b) \(\frac{{AM}}{{AD}} + \frac{{CN}}{{CB}} = 1\).
Độ dài x trong Hình 5.13 là

A. 20
B. 50
C. 12
D. 30
Cho hình thang ABCD (AB//DC). Gọi O là giao điểm của AC và BD. Xét các khẳng định sau:
(1) \(\frac{{OA}}{{OC}} = \frac{{OD}}{{OB}}\)
(2) \(OA.OD = OB.OC\)
(3) \(\frac{{AO}}{{AC}} = \frac{{BO}}{{BD}}\)
Số khẳng định đúng là:
A. 0
B. 1
C. 2
D. 3
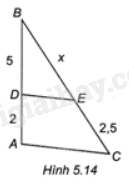
Cho Hình 5.14, biết DE//AC. Độ dài x là
A. 5
B. 7
C. 6,5
D. 6,25
Cho Hình 5.15, biết \(ED \bot AB,AC \bot AB.\) Khi đó, x có giá trị là

A. 2,5
B. 2
C. 3
D. 4
Cho hình bình hành ABCD, điểm E thuộc cạnh AB (E khác A và B), điểm F thuộc cạnh AD (F khác A và D). Đường thẳng qua D song song với EF cắt AC tại I. Đường thẳng qua B song song với EF cắt AC tại K.
a) Chứng minh rằng \(AI = CK\).
b) Gọi N là giao điểm của EF và AC. Chứng minh rằng: \(\frac{{AB}}{{AE}} + \frac{{AD}}{{AF}} = \frac{{AC}}{{AN}}\).
Cho góc nhọn xOy. Trên cạnh Ox lấy điểm N, trên cạnh Oy lấy điểm M. Gọi I là một điểm trên đoạn thẳng MN. Qua I kẻ đường thẳng song song với Ox cắt Oy tại A (A khác M và N) và đường thẳng song song với Oy cắt Ox ở B. Chứng minh rằng \(\frac{{MA}}{{MO}} + \frac{{NB}}{{NO}} = 1\)
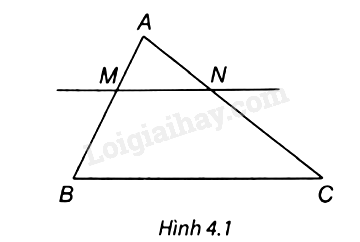
Quan sát Hình 4.1 biết MN // BC. Tỉ số \(\frac{{AM}}{{MB}}\) bằng
A. \(\frac{{AN}}{{AC}}\)
B. \(\frac{{AN}}{{NC}}\)
C. \(\frac{{NC}}{{AN}}\)
D. \(\frac{{BM}}{{AB}}\)
Quan sát Hình 4.2 và chọn khẳng định đúng.
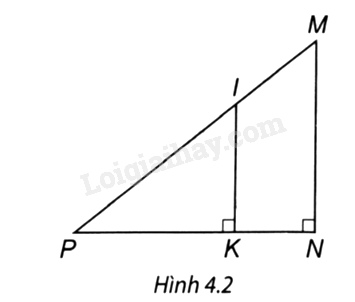
A. \(\frac{{PI}}{{PM}} = \frac{{KN}}{{PN}}.\)
B. \(\frac{{IM}}{{IP}} = \frac{{KP}}{{PN}}.\)
C. \(\frac{{MI}}{{MP}} = \frac{{NK}}{{NP}}.\)
D. \(\frac{{PI}}{{PM}} = \frac{{PK}}{{KN}}.\)
Quan sát Hình 4.3. Biết DE // BC, AD = 12, DB = 18, CE = 30. Độ dài AC bằng:

A. 20.
B. 56.
C. 45.
D. 50.
Tìm độ dài x, y trong Hình 4.4 (làm tròn kết quả đến chữ số thập phân thứ nhất).

Cho ∆ABC, từ điểm D trên cạnh BC, kẻ đường thẳng song song với AB cắt AC tại F và kẻ đường thẳng song song với AC cắt AB tại E. Chứng minh rằng: \(\frac{{AE}}{{AB}} + \frac{{AF}}{{AC}} = 1.\)
Cho ∆ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB, d cắt BC tại điểm M. Chứng minh rằng \(BM = \frac{1}{3}BC.\)
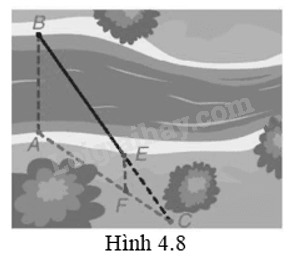
Để đo khoảng cách giữa hai vị trí B và E ở hai bên bờ sông, bác An chọn ba vị trí A, F, C cùng nằm ở một bên bờ sông sao cho ba điểm C, E, B thẳng hàng, ba điểm C, F, A thẳng hàng và AB // EF (H.4.8). Sau đó bác An đo được AF = 40 m, FC = 20 m, EC = 30 m. Hỏi khoảng cách giữa hai vị trí B và E bằng bao nhiêu?
Cho hình thang ABCD (AB // DC), AC cắt BD tại I. Chứng minh rằng IA . ID = IB . IC.
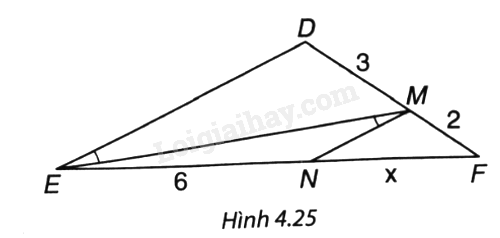
Tìm độ dài x trong Hình 4.25.
Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K. Chứng minh rằng: DM2 = MN.MK.









Danh sách bình luận