Tìm \(\mathop {\lim }\limits_{n \to + \infty } \frac{{1 + 3 + 5 + ... + \left( {2n - 1} \right)}}{{{n^2} + 2n}}\).
Để tính giới hạn của dãy số dạng phân thức, ta chia cả tử thức và mẫu thức cho lũy thừa cao nhất của n, rồi áp dụng các quy tắc tính giới hạn.
\(\mathop {\lim }\limits_{n \to + \infty } \frac{{1 + 3 + 5 + ... + \left( {2n - 1} \right)}}{{{n^2} + 2n}} = \mathop {\lim }\limits_{n \to + \infty } \frac{{{n^2}}}{{{n^2} + 2n}} = \mathop {\lim }\limits_{n \to + \infty } \frac{1}{{1 + \frac{2}{n}}} = 1\)

Các bài tập cùng chuyên đề
Tính \(\mathop {lim}\limits_{n \to + \infty } \left( {n - \sqrt n } \right)\).
Một loại vi khuẩn được nuôi cấy với số lượng ban đầu là 50. Sau mỗi chu kỳ 4 giờ, số lượng của chúng sẽ tăng gấp đôi.
a) Dự đoán công thức tính số vi khuẩn \({u_n}\) sau chu kì thứ n
b) Sau bao lâu, số lượng vi khuẩn sẽ vượt con số 10 000?
Tìm giới hạn của các dãy số cho bởi
a) \({u_n} = \frac{{{n^2} + 1}}{{2n - 1}}\)
b) \({v_n} = \sqrt {2{n^2} + 1} - n\)
Quan sát dãy số \((u_n)\) với \(u_n = n^2\) và cho biết giá trị của n có thể lớn hơn một số dương bất kì được hay không kể từ một số hạng nào đó trở đi.
Chứng tỏ rằng \(\lim \frac{{n - 1}}{{{n^2}}} = 0.\)
Tính \(\lim \left( { - {n^3}} \right).\)
Dựng một dãy hình vuông bằng cách ghép từ các hình vuông đơn vị (cạnh bằng 1 đơn vị độ dài) theo các bước như Hình 4. Kí hiệu \({u_n}\) (đơn vị diện tích) là diện tích hình vuông dựng được ở bước thứ \(n\).
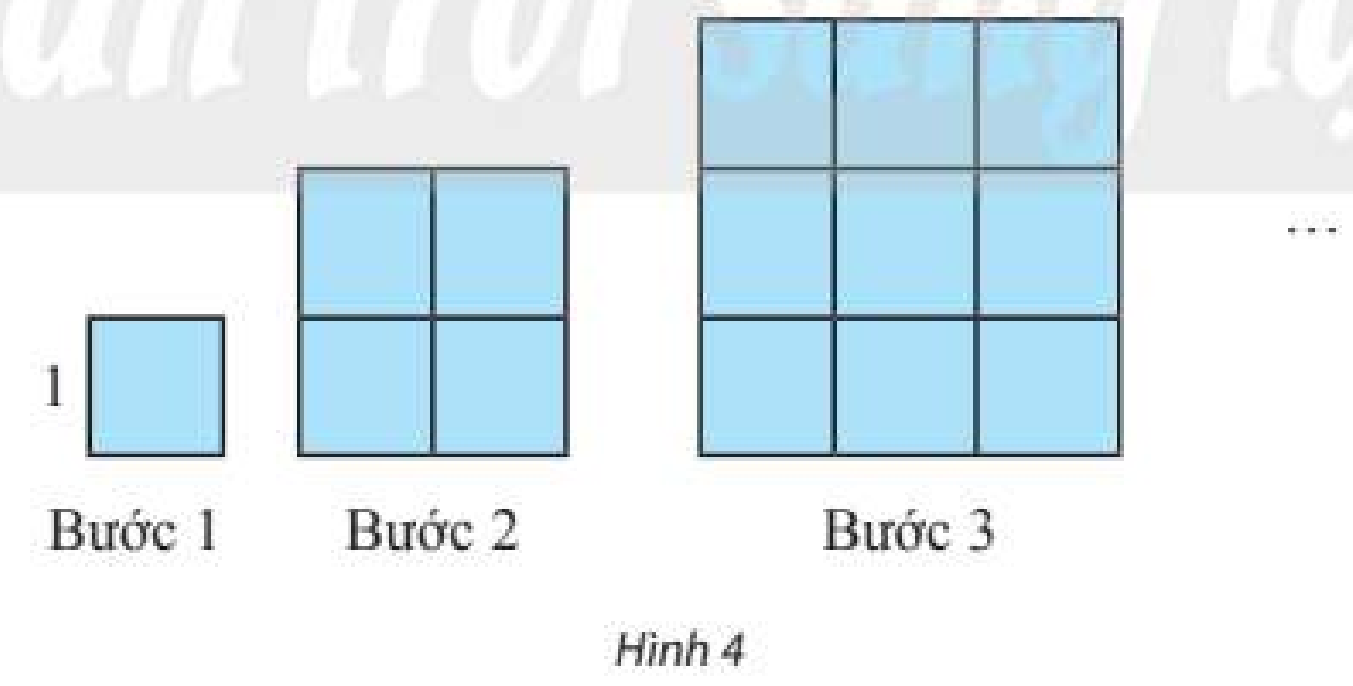
a) Với \(n\) như thế nào thì \({u_n}\) vượt quá 10000; 1000000?
b) Cho hình có diện tích \(S\). Với \(n\) như thế nào thì \({u_n}\) vượt quá \(S\)?
Tìm các giới hạn sau:
a) \(\lim \left( {1 + 3n - {n^2}} \right)\);
b) \(\lim \frac{{{n^3} + 3n}}{{2n - 1}}\);
c) \(\lim \left( {\sqrt {{n^2} - n} + n} \right)\);
d) \(\lim \left( {{3^{n + 1}} - {5^n}} \right)\).
Phát biểu nào sau đây là SAI?
A. Nếu \(\lim {u_n} = + \infty \) và \(\lim {v_n} = C\), \(C > 0\) thì \(\lim \frac{{{u_n}}}{{{v_n}}} = + \infty \).
B. Nếu \(\lim {u_n} = - \infty \) và \(\lim {v_n} = C\), \(C < 0\) thì \(\lim \frac{{{u_n}}}{{{v_n}}} = + \infty \).
C. Nếu \(\lim {u_n} = + \infty \) và \(\lim {v_n} = C\), \(C < 0\) thì \(\lim \frac{{{u_n}}}{{{v_n}}} = 0\).
D. Nếu \(\lim {u_n} = - \infty \) và \(\lim {v_n} = C\), \(C > 0\) thì \(\lim \frac{{{u_n}}}{{{v_n}}} = - \infty \).
Nếu \(\lim {u_n} = C\) và \(\lim {v_n} = + \infty \) (hoặc \(\lim {v_n} = - \infty \)) thì \(\lim \frac{{{u_n}}}{{{v_n}}}\) bằng:
A. \(0\)
B. \( - \infty \)
C. \( + \infty \)
D. \( - \infty \) hoặc \( + \infty \)
Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{n \to + \infty } \left( {\sqrt {{n^2} + 2n} - n - 2} \right);\)
b) \(\mathop {\lim }\limits_{n \to + \infty } \left( {2 + {n^2} - \sqrt {{n^4} + 1} } \right);\)
c) \(\mathop {\lim }\limits_{n \to + \infty } \left( {\sqrt {{n^2} - n + 2} + n} \right);\)
d) \(\mathop {\lim }\limits_{n \to + \infty } \left( {3n - \sqrt {4{n^2} + 1} } \right).\)
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{\cos n}}{{{n^2}}}.\) Tìm \(\mathop {\lim }\limits_{n \to + \infty } {u_n}\).







Danh sách bình luận