Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{n \to + \infty } \left( {\sqrt {{n^2} + 2n} - n - 2} \right);\)
b) \(\mathop {\lim }\limits_{n \to + \infty } \left( {2 + {n^2} - \sqrt {{n^4} + 1} } \right);\)
c) \(\mathop {\lim }\limits_{n \to + \infty } \left( {\sqrt {{n^2} - n + 2} + n} \right);\)
d) \(\mathop {\lim }\limits_{n \to + \infty } \left( {3n - \sqrt {4{n^2} + 1} } \right).\)
+ Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a\) và \(\mathop {\lim }\limits_{n \to + \infty } {v_n} = + \infty \) (hoặc \(\mathop {\lim }\limits_{n \to + \infty } {v_n} = - \infty \)) thì \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = 0\)
+ Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a > 0\) và \(\mathop {\lim }\limits_{n \to + \infty } {v_n} = 0\) và \({v_n} > 0\) với mọi n thì \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = + \infty \)
+ Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty \) và \(\mathop {\lim }\limits_{n \to + \infty } {v_n} = a > 0\) thì \(\mathop {\lim }\limits_{n \to + \infty } {u_n}{v_n} = + \infty \)
a) \(\mathop {\lim }\limits_{n \to + \infty } \left( {\sqrt {{n^2} + 2n} - n - 2} \right) = \mathop {\lim }\limits_{n \to + \infty } \frac{{ - 2n - 4}}{{\sqrt {{n^2} + 2n} + n + 2}} = \mathop {\lim }\limits_{n \to + \infty } \frac{{ - 2 - \frac{4}{n}}}{{\sqrt {1 + \frac{2}{n}} + 1 + \frac{2}{n}}} = - 1\)
b) \(\mathop {\lim }\limits_{n \to + \infty } \left( {2 + {n^2} - \sqrt {{n^4} + 1} } \right) = \mathop {\lim }\limits_{n \to + \infty } \frac{{4{n^2} + 3}}{{2 + {n^2} + \sqrt {{n^4} + 1} }} = \mathop {\lim }\limits_{n \to + \infty } \frac{{4 + \frac{3}{{{n^2}}}}}{{\frac{2}{{{n^2}}} + 1 + \sqrt {1 + \frac{1}{{{n^4}}}} }} = 2\)
c) \(\mathop {\lim }\limits_{n \to + \infty } \left( {\sqrt {{n^2} - n + 2} + n} \right) = \mathop {\lim }\limits_{n \to + \infty } n\left( {\sqrt {1 - \frac{1}{n} + \frac{2}{{{n^2}}}} + 1} \right) = + \infty \)
d) \(\mathop {\lim }\limits_{n \to + \infty } \left( {3n - \sqrt {4{n^2} + 1} } \right) = \mathop {\lim }\limits_{n \to + \infty } n\left( {3 - \sqrt {4 + \frac{1}{{{n^2}}}} } \right) = + \infty \)

Các bài tập cùng chuyên đề
Tính \(\mathop {lim}\limits_{n \to + \infty } \left( {n - \sqrt n } \right)\).
Một loại vi khuẩn được nuôi cấy với số lượng ban đầu là 50. Sau mỗi chu kỳ 4 giờ, số lượng của chúng sẽ tăng gấp đôi.
a) Dự đoán công thức tính số vi khuẩn \({u_n}\) sau chu kì thứ n
b) Sau bao lâu, số lượng vi khuẩn sẽ vượt con số 10 000?
Tìm giới hạn của các dãy số cho bởi
a) \({u_n} = \frac{{{n^2} + 1}}{{2n - 1}}\)
b) \({v_n} = \sqrt {2{n^2} + 1} - n\)
Quan sát dãy số \((u_n)\) với \(u_n = n^2\) và cho biết giá trị của n có thể lớn hơn một số dương bất kì được hay không kể từ một số hạng nào đó trở đi.
Chứng tỏ rằng \(\lim \frac{{n - 1}}{{{n^2}}} = 0.\)
Tính \(\lim \left( { - {n^3}} \right).\)
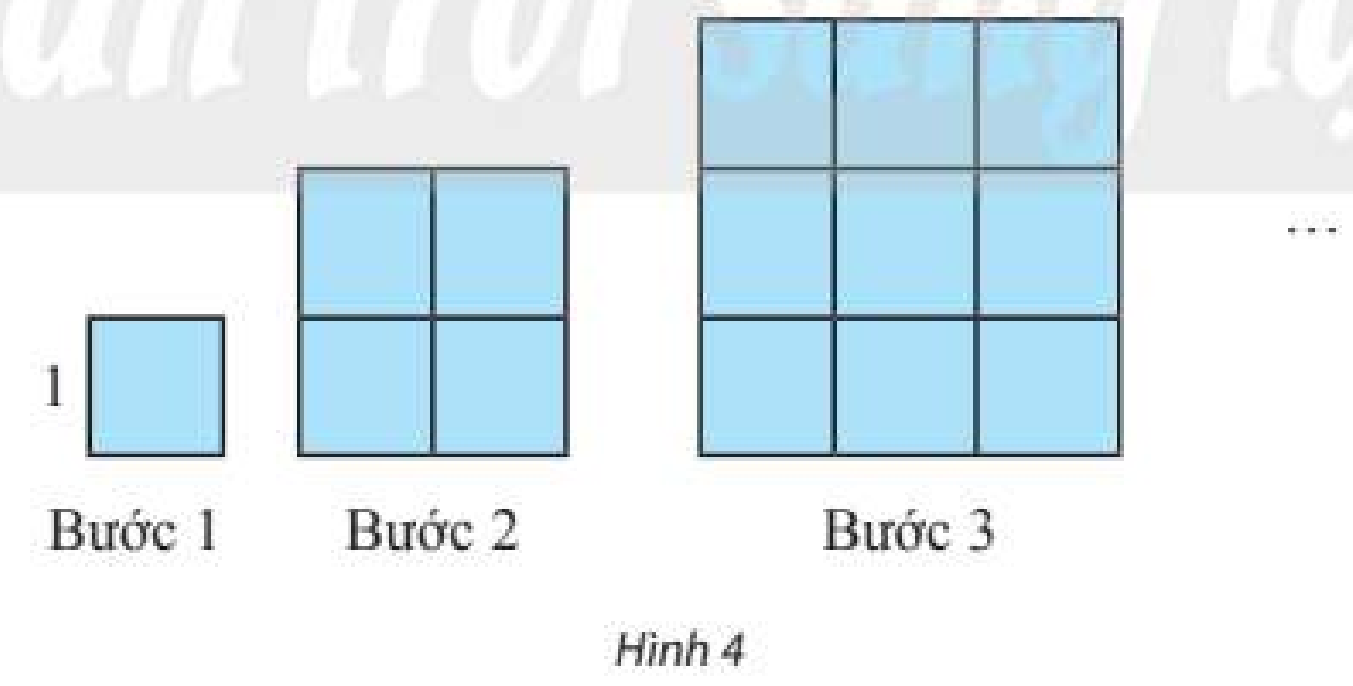
Dựng một dãy hình vuông bằng cách ghép từ các hình vuông đơn vị (cạnh bằng 1 đơn vị độ dài) theo các bước như Hình 4. Kí hiệu \({u_n}\) (đơn vị diện tích) là diện tích hình vuông dựng được ở bước thứ \(n\).
a) Với \(n\) như thế nào thì \({u_n}\) vượt quá 10000; 1000000?
b) Cho hình có diện tích \(S\). Với \(n\) như thế nào thì \({u_n}\) vượt quá \(S\)?
Tìm các giới hạn sau:
a) \(\lim \left( {1 + 3n - {n^2}} \right)\);
b) \(\lim \frac{{{n^3} + 3n}}{{2n - 1}}\);
c) \(\lim \left( {\sqrt {{n^2} - n} + n} \right)\);
d) \(\lim \left( {{3^{n + 1}} - {5^n}} \right)\).
Phát biểu nào sau đây là SAI?
A. Nếu \(\lim {u_n} = + \infty \) và \(\lim {v_n} = C\), \(C > 0\) thì \(\lim \frac{{{u_n}}}{{{v_n}}} = + \infty \).
B. Nếu \(\lim {u_n} = - \infty \) và \(\lim {v_n} = C\), \(C < 0\) thì \(\lim \frac{{{u_n}}}{{{v_n}}} = + \infty \).
C. Nếu \(\lim {u_n} = + \infty \) và \(\lim {v_n} = C\), \(C < 0\) thì \(\lim \frac{{{u_n}}}{{{v_n}}} = 0\).
D. Nếu \(\lim {u_n} = - \infty \) và \(\lim {v_n} = C\), \(C > 0\) thì \(\lim \frac{{{u_n}}}{{{v_n}}} = - \infty \).
Nếu \(\lim {u_n} = C\) và \(\lim {v_n} = + \infty \) (hoặc \(\lim {v_n} = - \infty \)) thì \(\lim \frac{{{u_n}}}{{{v_n}}}\) bằng:
A. \(0\)
B. \( - \infty \)
C. \( + \infty \)
D. \( - \infty \) hoặc \( + \infty \)
Tìm \(\mathop {\lim }\limits_{n \to + \infty } \frac{{1 + 3 + 5 + ... + \left( {2n - 1} \right)}}{{{n^2} + 2n}}\).
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{\cos n}}{{{n^2}}}.\) Tìm \(\mathop {\lim }\limits_{n \to + \infty } {u_n}\).







Danh sách bình luận