Cho hai hình vuông có chung cạnh\(AB\) và nằm trong hai mặt phẳng khác nhau. Trên các đường chéo \(AC\) và \(BF\) ta lấy các điểm \(M,N\)sao cho \(AM = BN\). Mặt phẳng \(\left( P \right)\) chứa \(MN\)và song song với \(AB\) cắt \(AD\) và \(AF\) lần lượt tại \(M',N'\). Khẳng định nào sau đây đúng?
-
A.
\(AC,BF\) cắt nhau.
-
B.
Tứ giác \(MNM'N'\) là hình bình hành.
-
C.
\(MN\) song song với \(\left( {DEF} \right)\).
-
D.
\(MN\) cắt \(\left( {DEF} \right)\).
Sử dụng các định lí:
‒ Cho đường thẳng \(a\) song song mặt phẳng \(\left( P \right)\). Nếu mặt phẳng \(\left( Q \right)\) chứa \(a\), cắt \(\left( P \right)\) theo giao tuyến \(b\) thì \(a\) song song với \(b\).
‒ Định lí Thalès trong tam giác: Nếu một đường thẳng song song với một cạnh của tam giác đó và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
‒ Nếu đường thẳng \(a\) không nằm trong mặt phẳng \(\left( P \right)\) và song song với một đường thẳng \(b\) nào đó nằm trong \(\left( P \right)\) thì \(a\) song song với \(\left( P \right)\).
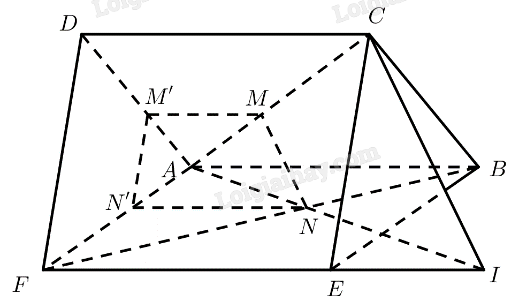
Gọi \(I = AN \cap EF\).
\(C{\rm{D}}\parallel EF\left( {\parallel AB} \right) \Rightarrow C,D,E,F\) đồng phẳng.
Theo định lí Thalès ta có:
\(MM'\parallel CD \Rightarrow \frac{{AM'}}{{AD}} = \frac{{AM}}{{AC}};NN'\parallel AB \Rightarrow \frac{{AN'}}{{AF}} = \frac{{BN}}{{BF}}\)
Mà \(AC = BF;AM = BN \Rightarrow \frac{{AM}}{{AC}} = \frac{{BN}}{{BF}}\)(1)
Theo định lí Thalès ta có:
\(AB\parallel FI \Rightarrow \frac{{BN}}{{NF}} = \frac{{AN}}{{NI}} \Rightarrow \frac{{BN}}{{BN + NF}} = \frac{{AN}}{{AN + NI}} \Rightarrow \frac{{BN}}{{BF}} = \frac{{AN}}{{AI}}\)(2)
Từ (1) và (2) suy ra
\(\left. \begin{array}{l}\frac{{AM}}{{AC}} = \frac{{AN}}{{AI}} \Rightarrow MN\parallel CI\\CI \subset \left( {DEF} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {DEF} \right)\)
Đáp án : C

Các bài tập cùng chuyên đề
Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b?
Nếu đường thẳng \(d\) không nằm trên mặt phẳng \(\left( P \right)\) và song song với một đường thẳng nằm trên \(\left( P \right)\) thì:
Cho hai đường thẳng phân biệt \(a,b\) và mặt phẳng \(\left( \alpha \right)\). Giả sử \(a\parallel \,b,b\parallel \,\left( \alpha \right)\). Khi đó:
Cho hai đường thẳng \(a\) và \(b\) cùng song song với mặt phẳng \(\left( P \right)\). Khẳng định nào sau đây đúng?
Cho \(\left\{ \begin{array}{l}a\parallel \left( \alpha \right)\\a \subset \left( \beta \right)\\d = \left( \alpha \right) \cap \left( \beta \right)\end{array} \right.\)thì khi đó:
Cho một điểm A nằm ngoài mặt phẳng (P). Có bao nhiêu đường thẳng qua A và song song với (P)?
Cho một mặt phẳng (P) và hai đường thẳng song song a, b. Mệnh đề nào đúng trong các mệnh đề sau?
(1) Nếu (P) // a thì (P) // b.
(2) Nếu (P) // a thì (P) // b hoặc chứa b.
(3) Nếu (P) // athì (P) cắt b.
(4) Nếu (P) cắt a thì (P) cũng cắt b.
(5) Nếu (P) cắt a thì (P) có thể song song với b.
(6) Nếu (P) chứa a thì có thể (P) song song với b.
Cho mặt phẳng \(\left( P \right)\) và hai đường thẳng \(a\) và \(b\) song song với nhau. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) \(a\parallel \left( P \right) \Rightarrow b\parallel \left( P \right)\).
(2) \(a\parallel \left( P \right) \Rightarrow b \subset \left( P \right)\).
(3) \(a\parallel \left( P \right) \Rightarrow \left[ \begin{array}{l}b\parallel \left( P \right)\\b \subset \left( P \right)\end{array} \right.\).
(4) Nếu \(\left( P \right)\) cắt \(a\) thì \(\left( P \right)\) cũng cắt \(b\).
(5) Nếu \(\left( P \right)\) cắt \(a\) thì \(\left( P \right)\) có thể song song với \(b\).
(6) Nếu \(\left( P \right)\) chứa \(a\) thì \(\left( P \right)\) có thể song song với \(b\).
Cho đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) song song với nhau. Khi đó số đường thẳng phân biệt nằm trong \(\left( P \right)\) song song với \(a\) là:
Cho tứ diện \(ABCD.\) Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AB\) và \(BC\). Đường thẳng \(MN\) song song với mặt phẳng nào dưới đây ?
Cho tứ diện \(ABCD\). Gọi \(M,N,P\) lần lượt là trung điểm của \(AB,AC,AD\). Trong các đường thẳng sau, đường thẳng nào không song song với \(\left( {BCD} \right)\)?
Cho tứ diện \(ABCD\). Gọi \(G\) là trọng tâm tam giác \(ACD\), \(M\) thuộc đoạn thẳng \(BC\) sao cho \(CM = 2MB\). Chọn mệnh đề đúng trong các mệnh đề sau?
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của AB, CD, SA. Trong các mệnh đề sau, mệnh đề nào đúng?
Cho hai hình bình hành \(ABCD\) và \(ABEF\) lần lượt có tâm \({O_1},{O_2}\) và không cùng nằm trong một mặt phẳng. Mệnh đề nào sau đây sai?
Cho tứ diện \(ABCD\). Gọi \(M,N\) lần lượt là trung điểm của \(AB,AC\). Gọi \(d\) là giao tuyến của hai mặt phẳng \(\left( {DMN} \right)\) và \(\left( {DBC} \right)\). Xét vị trí tương đối của \(d\) và \(\left( {ABC} \right)\).
Cho lăng trụ \(ABC.A'B'C'\). Gọi \(I\) là trung điểm của \(B'C'\). Khẳng định nào sau đây là đúng?
Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(I\) là trung điểm của \(AB'\). Khẳng định nào sau đây là đúng?
Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành. Một mặt phẳng (P) đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD và BD tại M, N, E, F, I, J. Khi đó ta có:
Cho tứ diện \(ABCD\). \(M\) là điểm nằm trong tam giác \(ABC\), mặt phẳng \(\left( \alpha \right)\) qua \(M\) và song song với \(AB\) và \(CD\). Thiết diện của \(ABCD\) cắt bởi mặt phẳng \(\left( \alpha \right)\) là:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Mặt phẳng \(\left( \alpha \right)\) qua \(B{\rm{D}}\) và song song với \(SA\), mặt phẳng \(\left( \alpha \right)\) cắt \(SC\) tại \(K\). Khẳng định nào sau đây là khẳng định đúng?






