Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(I\) là trung điểm của \(AB'\). Khẳng định nào sau đây là đúng?
-
A.
\(C'I\parallel \left( {BCD'} \right)\).
-
B.
\(C'I\parallel \left( {ACD'} \right)\).
-
C.
\(C'I\parallel AC\).
-
D.
\(C'I\parallel BC\).
Sử dụng định lí: Nếu đường thẳng \(a\) không nằm trong mặt phẳng \(\left( P \right)\) và song song với một đường thẳng \(b\) nào đó nằm trong \(\left( P \right)\) thì \(a\) song song với \(\left( P \right)\).
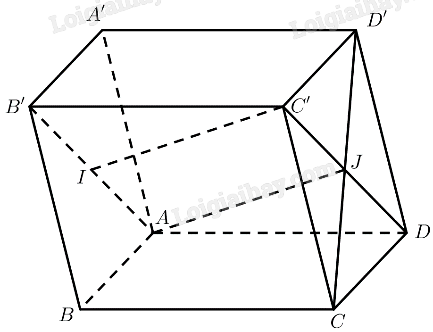
Gọi \(J\) là giao điểm của \(CD'\) và \(C'D\)
\( \Rightarrow J\) là trung điểm của \(C'D\)
\(A{\rm{D}}\parallel B'C',A{\rm{D}} = B'C'\) \( \Rightarrow ADC'B'\) là hình bình hành
\(\left. \begin{array}{l} \Rightarrow AB' = C'D,AB'\parallel C'D\\IA = \frac{1}{2}AB',JC' = \frac{1}{2}C'D\end{array} \right\} \Rightarrow IA = C'J\)
Mà \(AB'\parallel C'D \Rightarrow IA\parallel C'J\)\( \Rightarrow AIC'J\) là hình bình hành
\(\left. \begin{array}{l} \Rightarrow C'I\parallel AJ\\AJ \subset \left( {ACD'} \right)\end{array} \right\} \Rightarrow C'I\parallel \left( {ACD'} \right)\)
Đáp án : B
