Đề bài
Quan sát trục số sau:
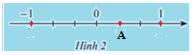
Điểm A biểu diễn số hữu tỉ nào?
-
A.
\(3\)
-
B.
\(\dfrac{1}{3}\)
-
C.
\(\dfrac{{ - 1}}{3}\)
-
D.
\(\dfrac{4}{3}\)
Phương pháp giải
+ Đếm số phần bằng nhau đoạn thẳng đơn vị chia ra.
+ Đếm khoảng cách từ O đến A bằng bao nhiêu đơn vị mới.
+ Số hữu tỉ nằm bên phải gốc O biểu diễn số dương
Lời giải của GV Loigiaihay.com
1 đoạn thẳng đơn vị được chia thành 4 phần bằng nhau nên 1 đơn vị mới bằng \(\dfrac{1}{3}\) đơn vị cũ
Điểm A nằm bên phải gốc O, cách gốc O một đoạn bằng 1 đơn vị mới.
Vậy điểm A biểu diễn số hữu tỉ \(\dfrac{1}{3}\)
Đáp án : B








Danh sách bình luận