Biểu diễn các số \(\dfrac{1}{4};0,25;\dfrac{{ - 25}}{{ - 100}};\dfrac{5}{{20}}\) trên cùng một trục số, ta được bao nhiêu điểm phân biệt?
-
A.
1 điểm
-
B.
2 điểm
-
C.
3 điểm
-
D.
4 điểm
Các số hữu tỉ bằng nhau được biểu diễn bởi 1 điểm duy nhất trên trục số.
Ta kiểm tra xem các số hữu tỉ trên có bằng nhau không
Ta có:
\(\begin{array}{l}0,25 = \dfrac{{25}}{{100}} = \dfrac{{25:25}}{{100:25}} = \dfrac{1}{4};\\\dfrac{{ - 25}}{{ - 100}} = \dfrac{{ - 25:\left( { - 25} \right)}}{{ - 100:\left( { - 25} \right)}} = \dfrac{1}{4};\\\dfrac{5}{{20}} = \dfrac{{5:5}}{{20:5}} = \dfrac{1}{4}\end{array}\)
Vậy \(\dfrac{1}{4} = 0,25 = \dfrac{{ - 25}}{{ - 100}} = \dfrac{5}{{20}}\) nên chúng cùng biểu diễn bởi 1 điểm trên trục số.
Đáp án : A

Các bài tập cùng chuyên đề
Mỗi điểm A,B,C trên trục số Hình 1.4 biểu diễn số hữu tỉ nào?

Biểu diễn các số hữu tỉ \(\frac{5}{4}\) và \(\frac{{ - 5}}{4}\) trên trục số.
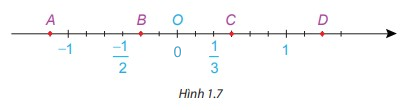
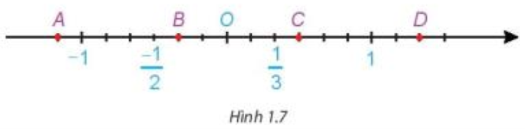
Các điểm A,B,C,D (H.1.7) biểu diễn những số hữu tỉ nào?
a) Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ -0,625?
\(\frac{5}{{ - 8}};\frac{{10}}{{16}};\frac{{20}}{{ - 32}};\frac{{ - 10}}{{16}};\frac{{ - 25}}{{40}};\frac{{35}}{{ - 48}}.\)
b) Biểu diễn số hữu tỉ -0,625 trên trục số.
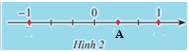
a) Biểu diễn các số nguyên -1;1;-2 trên trục số.
b) Quan sát Hình 2. Hãy dự đoán điểm A biểu diễn số hữu tỉ nào?
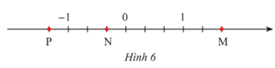
a) Các điểm M, N, P trong Hình 6 biểu diễn các số hữu tỉ nào?
b) Biểu diễn các số hữu tỉ sau trên trục số: \( - 0,75;\,\frac{1}{{ - 4}};\,1\frac{1}{4}.\)
a) Các điểm A,B,C trong Hình 8 biểu diễn số hữu tỉ nào?
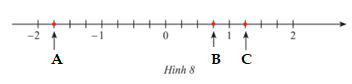
b) Biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số.
Biểu diễn số hữu tỉ \(\frac{7}{{10}}\) trên trục số
Biểu diễn số hữu tỉ -0,3 trên trục số
Quan sát trục số sau và cho biết các điểm A, B, C, D biểu diễn những số nào?

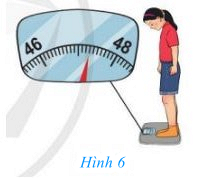
Bạn Linh đang cân khối lượng của mình (Hình 6), ở đó các vạch ghi 46 và 48 lần lượt ứng với các số đo 46 kg và 48 kg. Khi nhìn vị trí mà chiếc kim chỉ vào, bạn Minh đọc số đo là 47,15 kg, bạn Dương đọc số đo là 47,3 kg, bạn Quân đọc số đo là 47,65 kg. Bạn nào đã đọc đúng số đo? Vì sao?
Các điểm A, B, C, D (H.1.3) lần lượt biểu diễn các số hữu tỉ nào?

Hãy biểu diễn hai số hữu tỉ \( - \dfrac{4}{5}\) và \(\dfrac{1}{2}\) trên cùng một trục số.
a) Các điểm x, y, z trong hình dưới đây biểu diễn số hữu tỉ nào?

b) Biểu diễn các số hữu tỉ \(\dfrac{{ - 3}}{4}\);\(1\dfrac{1}{4}\);\(\dfrac{1}{4}\); -1,5 trên trục số.
Quan sát trục số ở Hình 5, điểm nào biểu diễn số hữu tỉ \(\dfrac{3}{4}\)?
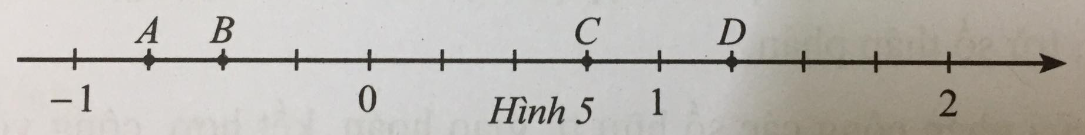
Điểm nào sau đây biểu diễn số hữu tỉ \(1\frac{3}{4}?\)

A. Điểm \(A\)
B. Điểm \(B\)
C. Điểm \(C\)
D. Điểm \(D\)
Các điểm \(A,B,C,D\) (h1.7) biểu diễn những số hữu tỉ nào?
Biểu diễn hai số hữu tỉ \(\frac{5}{3}\) và \(\frac{3}{2}\) trên trục số.
Khẳng định nào sau đây là sai?
A. Mỗi số hữu tỉ đều được biểu diễn bởi một điểm trên trục số;
B. Trên trục số, số hữu tỉ âm nằm bên trái điểm biểu diễn số 0;
C. Trên trục số, số hữu tỉ dương nằm bên phải điểm biểu diễn số 0;
D. Hai số hữu tỉ không phải luôn so sánh được với nhau.
Trong Hình 9, điểm nào biểu diễn số hữu tỉ \(\dfrac{3}{2}\) trên trục số?

A. Điểm M.
B. Điểm N.
C. Điểm P.
D. Điểm Q.
Biểu diễn các số hữu tỉ \(\frac{{ - 1}}{3};\frac{1}{6};1\) lần lượt bằng các điểm A, B, C trên trục số ở Hình 10.
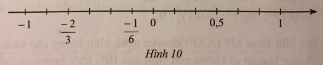
Số hữu tỉ \(\frac{3}{4}\) được biểu diễn bởi:
-
A.
Bốn điểm trên trục số;
-
B.
Ba điểm trên trục số;
-
C.
Hai điểm trên trục số;
-
D.
Một điểm duy nhất trên trục số.
Số hữu tỉ x nhỏ hơn số hữu tỉ y nếu trên trục số:
-
A.
Điểm x ở bên trái điểm y;
-
B.
Điểm x ở bên phải điểm y;
-
C.
Điểm x và điểm y khác phía đối với điểm 0;
-
D.
Cả 3 đáp án đều sai.
Các điểm X, Y, Z trong hình dưới đây biểu diễn số hữu tỉ nào?

-
A.
\(X = \frac{{ - 3}}{4}\);
-
B.
\(Y = \frac{{ - 1}}{2}\);
-
C.
\(Z = \frac{3}{4}\);
-
D.
Tất cả các đáp án trên đều đúng.
Điểm A trong hình dưới đây biểu diễn số hữu tỉ nào?

-
A.
\(\frac{2}{3}\);
-
B.
\(\frac{{ - 2}}{3}\);
-
C.
\(\frac{{ - 1}}{3}\);
-
D.
– 1.
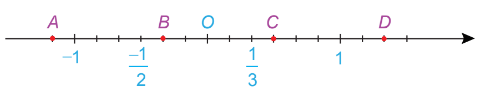
Các điểm B, C lần lượt biểu diễn những số hữu tỉ nào?
-
A.
\(\frac{1}{3}\), \(\frac{1}{2}\);
-
B.
\(\frac{{ - 1}}{3}\), \(\frac{1}{4}\);
-
C.
\(\frac{{ - 1}}{3}\), \(\frac{1}{2}\);
-
D.
\(\frac{{ - 1}}{3}\), \(\frac{1}{6}\).
Trên trục số, hai điểm biểu diễn của hai số hữu tỉ đối nhau
-
A.
nằm về cùng một phía so với điểm O;
-
B.
nằm về hai phía khác nhau so với điểm O;
-
C.
nằm về hai phía khác nhau so với điểm O và có cùng khoảng cách đến O;
-
D.
trùng nhau.
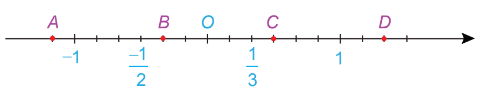
Điểm biểu diễn số đối của của số hữu tỉ \(\frac{{ - 1}}{2}\) là
-
A.
điểm A;
-
B.
điểm B;
-
C.
điểm C;
-
D.
điểm D.
Trên trục số, nếu a < b thì
-
A.
điểm a trùng với điểm b;
-
B.
điểm a nằm trước điểm b;
-
C.
điểm a nằm sau điểm b;
-
D.
điểm b nằm trước điểm a.
Cho hai số hữu tỉ a và b được biểu diễn trên trục số như sau

Khẳng định đúng nhất là
-
A.
b > 0 > a;
-
B.
b > a;
-
C.
b < a < 0;
-
D.
b < 0 < a.






