Bài 5. Dữ liệu Lôgic trang 11, 12 SBT Tin học 10 Kết nối tri thức với cuộc sống
Trong thực tế, có nhiều đối tượng có hai trạng thái đối lập đều có thể quy về đại lượng lôgic như giới tính (nam hay nữ), tình trạng hôn nhân (độc thân hay đang kết hôn)... Em hãy tìm thêm ba ví dụ khác.
5.1
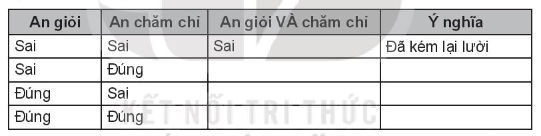
Em hãy điền vào ô trống trong bảng sau theo mẫu:
a)
b) Ở các trường đại học, sinh viên giỏi hoặc gia đình nghèo sẽ được cấp học bổng. Em hãy tính giá trị điều kiện được cấp học bổng.

Phương pháp giải:
Dựa vào kiến thức về các phép toán AND và OR trong bảng sau
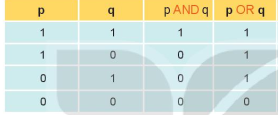
Lời giải chi tiết:
a)
|
An giỏi |
An chăm chỉ |
An giỏi VÀ chăm chỉ |
Ý nghĩa |
|
Sai |
Sai |
Sai |
Đã kém lại lười |
|
Sai |
Đúng |
Sai |
Không giỏi nhưng chăm chỉ |
|
Đúng |
Sai |
Sai |
Giỏi nhưng lười |
|
Đúng |
Đúng |
Đúng |
Vừa giỏi vừa chăm chỉ |
b)
|
Học giỏi |
Nghèo |
Học giỏi HOẶC nghèo |
Ý nghĩa |
|
Sai |
Sai |
Sai |
Không đủ tiêu chuẩn |
|
Sai |
Đúng |
Đúng |
Đủ tiêu chuẩn |
|
Đúng |
Sai |
Đúng |
Đủ tiêu chuẩn |
|
Đúng |
Đúng |
Đúng |
Đủ tiêu chuẩn |
5.2
Trong thực tế, có nhiều đối tượng có hai trạng thái đối lập đều có thể quy về đại lượng lôgic như giới tính (nam hay nữ), tình trạng hôn nhân (độc thân hay đang kết hôn)...
Em hãy tìm thêm ba ví dụ khác.
Phương pháp giải:
Dựa vào sự hiểu biết bản thân để tìm ví dụ
Lời giải chi tiết:
- Ảnh màu/ảnh đen trắng
- Đèn bật/tắt
- Tài liệu bản chính/bản sao
5.3
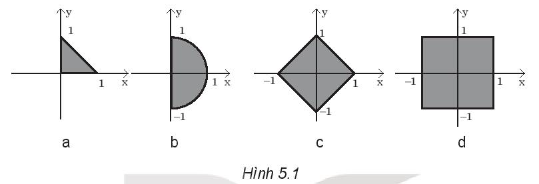
Một số hình vẽ trên mặt phẳng có thể biểu diễn qua các biểu thức lôgic có yếu tố toạ độ. Ví dụ Hình 5.1a được biểu diễn bởi biểu thức (x ≥ 0) AND (y ≥ 0) AND (x + y ≤ 1).
Em hãy viết biểu thức lôgic tương ứng với các Hình 5.1b, Hình 5.1c, Hình 5.1d
Phương pháp giải:
Biểu thức lôgic là một dãy các đại lượng lôgic được nối với nhau bằng các phép toán lôgic, có thể có dấu ngoặc để chỉ định thứ tự ưu tiên thực hiện các phép toán.
Dựa vào ví dụ Hình 5.1a để viết biểu thức lôgic
Lời giải chi tiết:
b) (x² + y² ≤ 1) AND (x ≥ 0)
c) |x|+ |y| ≤1
d) (|x|≤1) AND (|y|≤1)
5.4
Cho biểu thức lôgic (NOT x) AND (NOT y) như bảng sau. Em hãy cho biết kết quả nào sai?
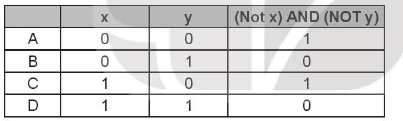
Phương pháp giải:
Dựa vào kiến thức về các phép toán trong bảng 5.2 - SGK
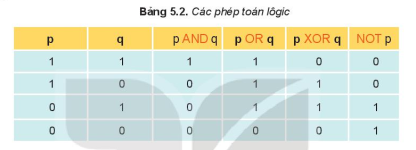
Lời giải chi tiết:
Kết quả sai: C
5.5
Em hãy tính giá trị của biểu thức lôgic (NOT x) AND (NOT y) với tất cả các bộ giá trị của x và y.
Phương pháp giải:
Dựa vào kiến thức về các phép toán trong bảng 5.2 - SGK
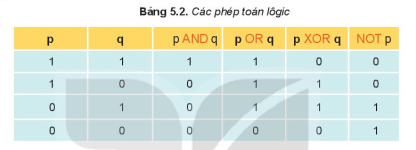
Lời giải chi tiết:
|
x |
y |
(NOT x) AND (NOT y) |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
5.6
Đố vui (Bài toán đoán màu mũ).
Chuyện rằng có 10 nhà thông thái (rất giỏi về suy luận lôgic) bị bọn cướp biển bắt được và giam trên đảo hoang. Chúng bịt mắt họ lại và đội lên đầu họ một chiếc mũ (đỏ hoặc xanh), sau đó bỏ băng bịt mắt. Mỗi người sẽ nhìn thấy và biết màu mũ của tất cả những người khác nhưng không biết màu mũ của mình.
Bọn cướp ra luật chơi, chúng sẽ hỏi từng người người xem họ đội mũ màu gì. Với điều kiện họ không được trao đổi với nhau, không được đoán mò, nếu chỉ một người đoán đúng, có cơ sở thì chúng sẽ tha tất, ngược lại sẽ tử hình toàn bộ.
Chúng hỏi nhà thông thái thứ nhất, ông nhìn tất cả những người còn lại và bảo không biết, không đủ cơ sở để biết màu mũ của mình.
Chúng lại hỏi thông thái thứ hai, anh ta cũng trả lời không đủ cơ sở để biết màu mũ của mình.
Lần lượt cả 9 nhà thông thái đều trả lời rằng không đủ cơ sở để biết màu mũ của mình.
Đến nhà thông thái thứ mười, ông nói ngay màu mũ của mình và giải thích cách suy luận. Bọn cướp khâm phục và thả tất cả các nhà thông thái.
Em có biết, nhà thông thái thứ 10 đã suy luận thế nào không?
Phương pháp giải:
Vận dụng kiến thức đã học trong bài
Lời giải chi tiết:
Bài toán đoán màu mũ.
- Gọi ai là mệnh đề "Các nhà thông thái (NTT) từ thứ i đến thứ 10 có cùng màu mũ".
- Theo giả thiết, có hai loại mũ nên a1 sai.
- NTT 1 không đoán được nên a2, cũng sai vì ngược lại, nếu NTT từ thứ 2 đến thứ 10 cùng một màu mũ thì NTT thứ nhất sẽ biết ngay là mình có màu mũ ngược lại. Tất cả mọi NTT đều biết điều này.
- NTT 2 biết điều này mà cũng không đoán được điều đó chứng tỏ a3, cũng sai. Tất cả mọi NTT đều biết điều này
- Cứ như vậy ta sẽ thấy tất cả a1, a2, a3... đến a9 đều sai, tức là màu mũ của NTT 9 và 10 là khác nhau. Vì vậy đến lượt mình, NTT 10 nhìn vào màu mũ của NTT 9 và bảo màu mũ của mình là mẫu ngược lại.
- Bài 6. Dữ liệu âm thanh và hình ảnh trang 14, 15 SBT Tin học 10 Kết nối tri thức với cuộc sống
- Bài 7. Thực hành sử dụng thiết bị số thông dụng 16, 17 SBT Tin học 10 Kết nối tri thức với cuộc sống
- Bài 4. Hệ nhị phân và dữ liệu số nguyên trang 9, 10 SBT Tin học 10 Kết nối tri thức với cuộc sống
- Bài 3. Một số kiểu dữ liệu và dữ liệu văn bản trang 8, 9 SBT Tin học 10 Kết nối tri thức với cuộc sống
- Bài 2. Vai trò của thiết bị thông minh và tin học đối với xã hội trang 6, 7 SBT Tin học 10 Kết nối tri thức với cuộc sống
>> Xem thêm
Các bài khác cùng chuyên mục
- Bài 34. Nghề phát triển phần mềm trang 69 SBT Tin học 10 Kết nối tri thức với cuộc sống
- Bài 33. Nghề thiết kế đồ hoạ máy tính trang 68 SBT Tin học 10 Kết nối tri thức với cuộc sống
- Bài 32. Ôn tập lập trình Python trang 66, 67 SBT Tin học 10 Kết nối tri thức với cuộc sống
- Bài 31. Thực hành viết chương trình đơn giản trang 63, 64 SBT Tin học 10 Kết nối tri thức với cuộc sống
- Bài 30. Kiểm thử và gỡ lỗi chương trình trang 61, 62 SBT Tin học 10 Kết nối tri thức với cuộc sống
- Bài 34. Nghề phát triển phần mềm trang 69 SBT Tin học 10 Kết nối tri thức với cuộc sống
- Bài 33. Nghề thiết kế đồ hoạ máy tính trang 68 SBT Tin học 10 Kết nối tri thức với cuộc sống
- Bài 32. Ôn tập lập trình Python trang 66, 67 SBT Tin học 10 Kết nối tri thức với cuộc sống
- Bài 31. Thực hành viết chương trình đơn giản trang 63, 64 SBT Tin học 10 Kết nối tri thức với cuộc sống
- Bài 30. Kiểm thử và gỡ lỗi chương trình trang 61, 62 SBT Tin học 10 Kết nối tri thức với cuộc sống













Danh sách bình luận