 Giải chuyên đề học tập Tin KNTT hay, chi tiết
Giải chuyên đề học tập Tin KNTT hay, chi tiết
 Chuyên đề 3: Thực hành thiết kế thuật toán theo kĩ thuậ..
Chuyên đề 3: Thực hành thiết kế thuật toán theo kĩ thuậ.. Bài 15: Bài toán xếp hậu - Chuyên đề Tin học 11 Kết nối tri thức
Trên bàn cờ vua chúng ta đều biết Hậu là quân cờ mạnh nhất vì nó có thể di chuyển theo tất cả các hướng ngang, dọc và chéo. Một bài toán vui rất nổi tiếng là tìm cách sắp xếp 8 quân Hậu trên bàn cờ sao cho không quân Hậu nào khống chế con nào. Em hãy thử tìm một cách xếp quân Hậu khác với cách xếp như hình sau:
Câu 1
Trả lời câu hỏi khởi động trang 63 Chuyên đề Tin học 11 Kết nối tri thức
Trên bàn cờ vua chúng ta đều biết Hậu là quân cờ mạnh nhất vì nó có thể di chuyển theo tất cả các hướng ngang, dọc và chéo. Một bài toán vui rất nổi tiếng là tìm cách sắp xếp 8 quân Hậu trên bàn cờ sao cho không quân Hậu nào khống chế con nào. Em hãy thử tìm một cách xếp quân Hậu khác với cách xếp như hình sau:
Lời giải chi tiết:
Bài toán tìm tất cả các cách xếp 8 quân Hậu trên bàn cờ vua sao cho các quân Hậu không khống chế lẫn nhau được gọi là bài toán xếp Hậu (n-Queen Problem). Bài toán này được nhà bác học Đức Carl Friedrich Gauss nghiên cứu từ 4 những năm 1850. Bài toán đã được mở rộng trên bàn cờ kích thước bất kì và vẫn đang được tiếp tục phát triển cho đến ngày nay.

Hình 15.1. Bàn cờ vua
Em có thể xếp như sau: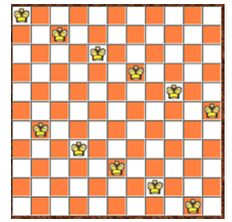
Câu 2
Trả lời câu hỏi hoạt động 1 trang 63 Chuyên đề Tin học 11 Kết nối tri thức
Đọc, quan sát, trao đổi và thảo luận về bài toán xếp Hậu tổng quát và cách tiếp cận quay lui để giải bài toán.
Lời giải chi tiết:
Trong quá trình quay lui, ta sử dụng một mảng để lưu vị trí của các quân hậu đã đặt. Mỗi lần thêm một quân hậu mới, ta kiểm tra xem nó có đặt được ở vị trí đó không bằng cách kiểm tra xem quân hậu mới đó có trùng hàng, cột hay đường chéo với bất kỳ quân hậu nào đã đặt trước đó không.
Nếu quân hậu mới đó không thể đặt được ở vị trí đó, ta quay lại đặt lại quân hậu trước đó tại một vị trí khác và tiếp tục thử các vị trí khác cho đến khi tìm được vị trí thích hợp.
Với phương pháp này, ta sẽ duyệt qua tất cả các trường hợp có thể có và đưa ra được kết quả đúng của bài toán.
Câu 3
Trả lời câu hỏi 1 trang 65 Chuyên đề Tin học 11 Kết nối tri thức
Giả sử n = 4, A[0] = 2, A[1] = 0. Hãy tìm A[2]
Lời giải chi tiết:
A[k] cần thỏa mãn điều kiện sau:
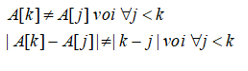
Do đó A[2] ≠ 0, 2 và | A[2]-2 | ≠2 và | A[2]-0 | ≠1 nên A[2] = 3
Do đó A[3] = 1
Câu 4
Trả lời câu hỏi 2 trang 65 Chuyên đề Tin học 11 Kết nối tri thức
Nếu n = 5, A[0] = 0, A[1] = 3. Tìm các khả năng của A[2]
Lời giải chi tiết:
A[k] cần thỏa mãn điều kiện sau:
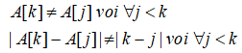
Do đó A[2] ≠ 0, 3 và | A[2]-2 | ≠2 và | A[2]-3 | ≠1 nên A[2] = 1
Câu 5
Trả lời câu hỏi hoạt động 2 trang 65 Chuyên đề Tin học 11 Kết nối tri thức
Đọc, quan sát, trao đổi và thảo luận về thuật toán và thiết lập chương trình hoàn chỉnh giải bài toán
Lời giải chi tiết:
* Thuật toán: Sử dụng kĩ thuật duyệt quay lui và in ra tất cả phương án nghiệm
* Thiết lập chương trình hoàn chỉnh giải bài toán.

Câu 6
Trả lời câu hỏi 1 trang 67 Chuyên đề Tin học 11 Kết nối tri thức
Với n = 3 bài toán xếp Hậu có nghiệm không?
Lời giải chi tiết:
Với n = 3, bài toán có nghiệm:

Câu 7
Trả lời câu hỏi 2 trang 67 Chuyên đề Tin học 11 Kết nối tri thức
Vì sao chương trình trên cần khai báo biến ncount với từ khoá global bên trong hàm trynext()
Lời giải chi tiết:
Biến ncount với từ khoá global bên trong hàm trynext() dùng để đếm số phương án thỏa mãn. Biến này được khởi tạo một lần và cập nhật giá trị nếu có phương án phù hợp. Sau khi được khởi tạo, giá trị của biến có thể thay đổi trong suốt quá trình chạy chương trình. Các hàm hoặc phương thức khác nhau trong chương trình có thể truy cập và thay đổi giá trị của biến global này.
Luyện tập Câu 1
Trả lời câu hỏi Luyện tập 1 trang 67 Chuyên đề Tin học 11 Kết nối tri thức
Hãy tìm bằng tay (không cần máy tính) cả hai phương án của bài toán xếp Hậu với n = 4
Lời giải chi tiết:
Hai phương án như sau:
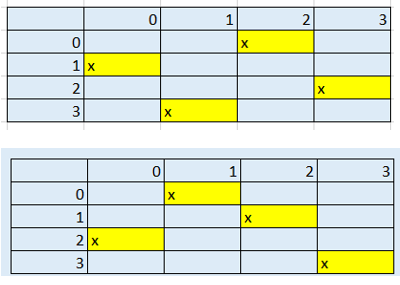
Luyện tập Câu 2
Trả lời câu hỏi Luyện tập 2 trang 67 Chuyên đề Tin học 11 Kết nối tri thức
Nếu chúng ta mô phỏng lưới ô vuông đánh chỉ số các hàng từ dưới lên thì chương trình trên còn đúng không? Nếu phải thay đổi thì cần sửa chỗ nào?
Lời giải chi tiết:
Nếu chúng ta mô phỏng lưới ô vuông đánh chỉ số các hàng từ dưới lên thì chương trình trên còn đúng không? Nếu phải thay đổi thì cần sửa chỗ nào?
Vận dụng Câu 1
Trả lời câu hỏi Vận dụng 1 trang 67 Chuyên đề Tin học 11 Kết nối tri thức
Gọi Q(n) là số các cách xếp n quân Hậu lên bàn cờ kích thước n x n sao cho các quân Hậu không khống chế nhau. Sử dụng thuật toán đã được học, em hãy viết chương trình tính các giá trị Q(n) với n = 4, 5, 6, 7, 8, 9, 10
Lời giải chi tiết:
Chương trình viết như sau:
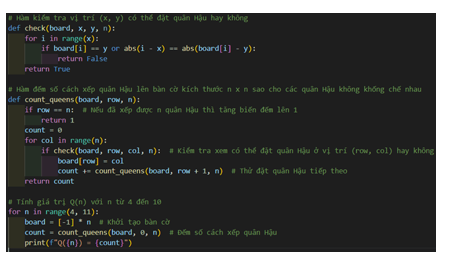
Thu được kết quả là:
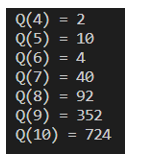
Vận dụng Câu 2
Trả lời câu hỏi Vận dụng 2 trang 67 Chuyên đề Tin học 11 Kết nối tri thức
Tính Q(n) với n = 11, 12, 13
Lời giải chi tiết:
Tương tự, thay đổi giá trị của n ta thu được kết quả sau:
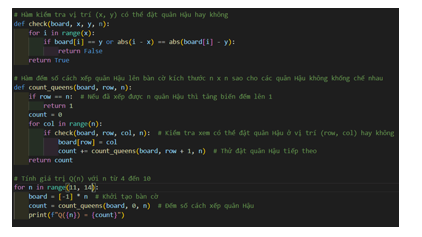
- Bài 16: Thực hành thiết kế thuật toán theo kĩ thuật quay lui - Chuyên đề Tin học 11 Kết nối tri thức
- Bài 14: Thực hành kĩ thuật duyệt quay lui - Chuyên đề Tin học 11 Kết nối tri thức
- Bài 12: Thực hành kĩ thuật duyệt cho bài toán tìm kiếm - Chuyên đề Tin học 11 Kết nối tri thức
- Bài 13: Kĩ thuật duyệt quay lui - Chuyên đề Tin học 11 Kết nối tri thức
- Bài 11: Bài toán tìm kiếm theo kĩ thuật duyệt - Chuyên đề Tin học 11 Kết nối tri thức
>> Xem thêm
Các bài khác cùng chuyên mục
- Bài 16: Thực hành thiết kế thuật toán theo kĩ thuật quay lui - Chuyên đề Tin học 11 Kết nối tri thức
- Bài 15: Bài toán xếp hậu - Chuyên đề Tin học 11 Kết nối tri thức
- Bài 14: Thực hành kĩ thuật duyệt quay lui - Chuyên đề Tin học 11 Kết nối tri thức
- Bài 12: Thực hành kĩ thuật duyệt cho bài toán tìm kiếm - Chuyên đề Tin học 11 Kết nối tri thức
- Bài 13: Kĩ thuật duyệt quay lui - Chuyên đề Tin học 11 Kết nối tri thức
- Bài 16: Thực hành thiết kế thuật toán theo kĩ thuật quay lui - Chuyên đề Tin học 11 Kết nối tri thức
- Bài 15: Bài toán xếp hậu - Chuyên đề Tin học 11 Kết nối tri thức
- Bài 14: Thực hành kĩ thuật duyệt quay lui - Chuyên đề Tin học 11 Kết nối tri thức
- Bài 12: Thực hành kĩ thuật duyệt cho bài toán tìm kiếm - Chuyên đề Tin học 11 Kết nối tri thức
- Bài 13: Kĩ thuật duyệt quay lui - Chuyên đề Tin học 11 Kết nối tri thức











Danh sách bình luận