Tổng hai góc đối của tứ giác nội tiếp bằng bao nhiêu độ? Cách tính góc của tứ giác nội tiếp - Toán 9

Tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (hoặc đơn giản là tứ giác nội tiếp) và đường tròn được gọi là đường tròn ngoại tiếp tứ giác.

Ví dụ:

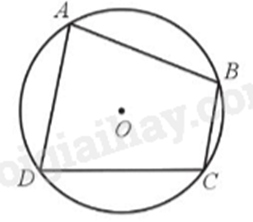
Tứ giác ABCD là tứ giác nội tiếp và đường tròn (O) được gọi là đường tròn ngoại tiếp tứ giác ABCD.

Trong một tứ giác nội tiếp đường tròn, tổng số đo hai góc đối bằng \(180^\circ \).

Ví dụ:

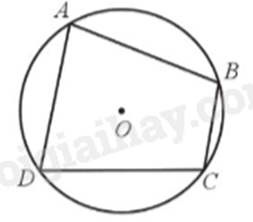
Tứ giác ABCD nội tiếp (O) nên \(\widehat A + \widehat C = 180^\circ ;\widehat B + \widehat D = 180^\circ \).

Dựa vào tính chất tổng số đo hai góc đối bằng \(180^\circ \).

Ngoài ra, ta cần nắm lại các kiến thức về góc nội tiếp, góc ở tâm.

Số đo của một cung được xác định như sau:

- Số đo của nửa đường tròn bằng \(180^\circ \).

- Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

- Số đo cung lớn bằng hiệu giữa \(360^\circ \) và số đo của cung nhỏ có chung hai mút.

Ví dụ: Số đo của cung AB được kí hiệu là sđ$\overset\frown{AB}$.

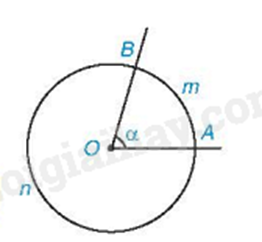
sđ$\overset\frown{AmB}=\widehat{AOB}=\alpha $; sđ$\overset\frown{AnB}=360{}^\circ -\alpha $.

Chú ý:

- Cung có số đo \(n^\circ \) còn được gọi là cung \(n^\circ \). Cả đường tròn được coi là cung \(360^\circ \). Đôi khi ta cũng coi một điểm là cung \(0^\circ \).

- Hai cung trên một đường tròn gọi là bằng nhau nếu chúng có cùng số đo.

- Trong một đường tròn, số đo của góc ở tâm bằng số đo của cung bị chắn.

- Trong một đường tròn, số đo của góc nội tiếp (nhỏ hơn hoặc bằng \(90^\circ \)) bằng nửa số đo cung bị chắn.

Như vậy, số đo góc nội tiếp (nhỏ hơn hoặc bằng \(90^\circ \)) bằng một nửa số đo góc ở tâm cùng chắn một cung.