Copyright © 2021 loigiaihay.com
Từ điển Toán 9 | Các dạng bài tập Toán 9
Hình quạt tròn và hình vành khuyên - Từ điển môn Toán 9
Hình quạt tròn và hình vành khuyên - Từ điển môn Toán 9 Hình vành khuyên là gì? Cách tính diện tích hình vành khuyên - Toán 9
1. Hình vành khuyên là gì?
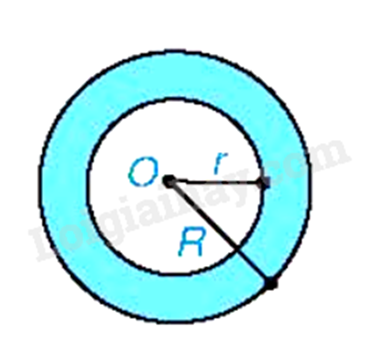
Hình vành khuyên (còn gọi là hình vành khăn) là phần nằm giữa hai đường tròn có cùng tâm và bán kính khác nhau (còn gọi là hai đường tròn đồng tâm)
2. Cách tính diện tích hình vành khuyên
Diện tích ${{S}_{v}}$ của hình vành khuyên tạo bởi hai đường tròn đồng tâm và có bán kính R và r:
${{S}_{v}}=\pi \left( {{R}^{2}}-{{r}^{2}} \right)$ (với R > r)
Tỉ số giữa diện tích hình quạt tròn ứng với cung $n{}^\circ $ và diện tích hình tròn (cùng bán kính) đúng bằng $\frac{n}{360}$ và bằng tỉ số giữa độ dài cung $n{}^\circ $ và độ dài đường tròn.
Ví dụ: Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 3m và 5m là:
${{S}_{v}}=\pi \left( {{5}^{2}}-{{3}^{2}} \right)=16\pi \left( {{m}^{2}} \right)$
3. Bài tập vận dụng
Các bài khác cùng chuyên mục
