Cách chứng minh một đường thẳng là tiếp tuyến của đường tròn - Toán 9

Nếu đường thẳng và đường tròn tiếp xúc nhau thì đường thẳng được gọi là tiếp tuyến của đường tròn, điểm chung được gọi là tiếp điểm.

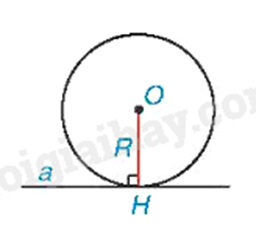
Điểm chung H của đường thẳng và đường tròn tiếp xúc với nhau goi là tiếp điểm.

Khi đó đường thẳng a còn gọi là tiếp tuyến của đường tròn (O) tại H.

Đường thẳng a tiếp xúc với đường tròn (O) tại H thì \(OH \bot a\).

Nếu một đường thẳng đi qua một điểm nằm trên một đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là tiếp tuyến của đường tròn.

Để chứng minh đường thẳng d là tiếp tuyến của đường tròn (O;R) tại tiếp điểm A, ta có thể làm theo cách sau:

Cách 1. Chứng minh \(OA \bot d\) tại A và \(A \in \left( O \right)\).

Cách 2. Vẽ \(OH \bot d\). Chứng minh \(OH \equiv OA = R\).

Cách 3. Vẽ tiếp tuyến \(d'\) của \(\left( O \right)\). Ta chứng minh \(d \equiv d'\).