Cách tính độ dài đoạn thẳng, góc liên quan đến tiếp tuyến của đường tròn - Toán 9

Nếu đường thẳng và đường tròn tiếp xúc nhau thì đường thẳng được gọi là tiếp tuyến của đường tròn, điểm chung được gọi là tiếp điểm.

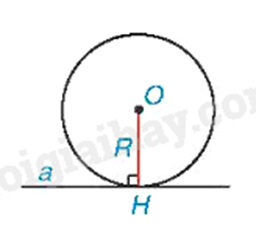
Điểm chung H của đường thẳng và đường tròn tiếp xúc với nhau goi là tiếp điểm.

Khi đó đường thẳng a còn gọi là tiếp tuyến của đường tròn (O) tại H.

Đường thẳng a tiếp xúc với đường tròn (O) tại H thì \(OH \bot a\).

Để chứng minh đường thẳng d là tiếp tuyến của đường tròn (O;R) tại tiếp điểm A, ta có thể làm theo cách sau:

Cách 1. Chứng minh \(OA \bot d\) tại A và \(A \in \left( O \right)\).

Cách 2. Vẽ \(OH \bot d\). Chứng minh \(OH \equiv OA = R\).

Cách 3. Vẽ tiếp tuyến \(d'\) của \(\left( O \right)\). Ta chứng minh \(d \equiv d'\).

Vận dụng kiến thức về tiếp tuyến và hệ thức lượng trong tam giác vuông để tính toán.