Hình quạt tròn là gì? Cách tính diện tích hình tròn. Cách tính diện tích hình quạt tròn - Toán 9

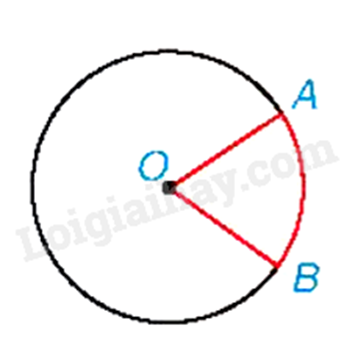
Hình quạt tròn là phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai đầu mút của cung đó.

Diện tích hình tròn bán kính R: $S=\pi {{R}^{2}}$.

Diện tích ${{S}_{q}}$ của hình quạt tròn bán kính R ứng với cung $n{}^\circ $:

${{S}_{q}}=\frac{n}{360}\pi {{R}^{2}}=\frac{l.R}{2}$

Ví dụ: Diện tích hình quạt tròn có độ dài tương ứng với nó là $l=4\pi $cm, bán kính là R = 5cm là:

${{S}_{q}}=\frac{l.R}{2}=\frac{4\pi .5}{2}=10\pi \left( c{{m}^{2}} \right)$