Bài 2. Phương trình dao động điều hòa trang 14, 15, 16, 17, 18, 19, 20, 21 Vật Lí 11 Chân trời sáng tạo
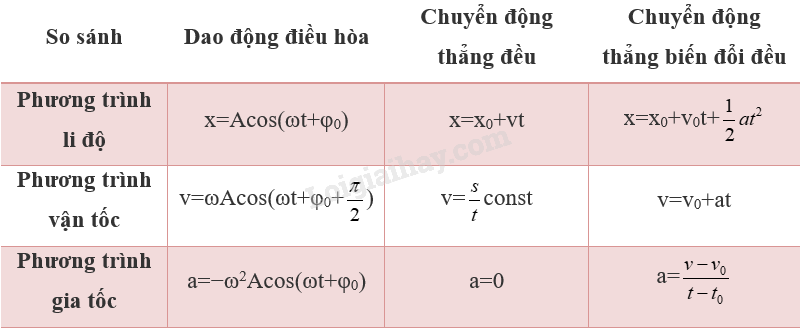
Việc nghiên cứu các quả trình dao động điều hoà để ứng dụng vào thực tiễn như xây dựng mô hình dự báo động đất yêu cầu ta phải mô tả chính xác trạng thái của vật dao động tại những thời điểm xác định. Ngoài ra, dao động điều hoà có tính chất tuần hoàn theo thời gian và bị giới hạn trong không gian thì phương trình li độ, vận tốc và gia tốc của vật dao động điều hoà có những khác biệt gì so với chuyển động thẳng đều và biến đổi đều mà em đã học ở chương trình Vật lí 10?
Câu hỏi tr 14 KĐ
Việc nghiên cứu các quả trình dao động điều hoà để ứng dụng vào thực tiễn như xây dựng mô hình dự báo động đất yêu cầu ta phải mô tả chính xác trạng thái của vật dao động tại những thời điểm xác định. Ngoài ra, dao động điều hoà có tính chất tuần hoàn theo thời gian và bị giới hạn trong không gian thì phương trình li độ, vận tốc và gia tốc của vật dao động điều hoà có những khác biệt gì so với chuyển động thẳng đều và biến đổi đều mà em đã học ở chương trình Vật lí 10?
Phương pháp giải:
Sử dụng những kiến thức đã được học
Lời giải chi tiết:
Câu hỏi tr 14 CH
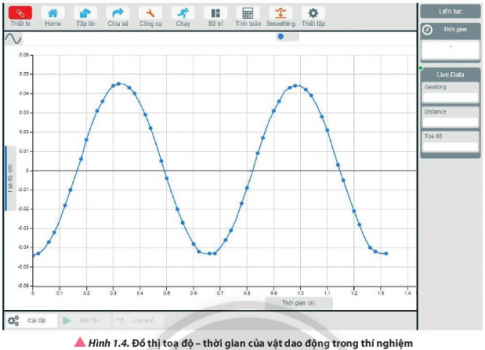
Quan sát dao động của con lắc lò xo và kết hợp với Hình 1.4, hãy chỉ rõ sự khác nhau giữa hình dạng quỹ đạo chuyển động và đồ thị li độ của vật dao động theo thời gian.
Phương pháp giải:
Áp dụng kiến thức đã học về quỹ đạo, hình dạng đồ thị hàm số
Lời giải chi tiết:
Quỹ đạo của vật dao động điều hòa là khoảng cách từ biên âm đến biên dương và ngược lại.
Còn hình dạng đồ thị li độ của vật dao động theo thời gian là một đường hình sin.
Câu hỏi tr 15 LT
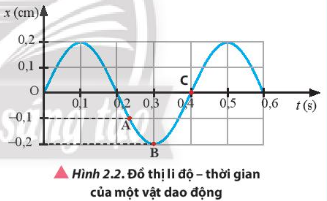
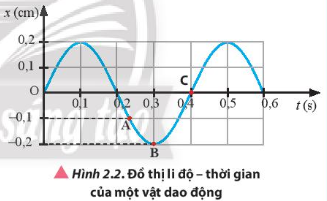
Một vật dao động có đồ thị li độ – thời gian được mô tả trong Hình 2.2. Hãy xác định:
a) Biên độ dao động, chu kì, tần số, tần số góc của dao động.
b) Li độ của vật dao động tại các thời điểm t1, t2, t3 ứng với các điểm A, B, C trên đường đồ thị li độ – thời gian.
c) Độ dịch chuyển so với vị trí ban đầu tại thời điểm t1, t2, t3 trên đường đồ thị.
Phương pháp giải:
Áp dụng kiến thức đã học, sử dụng công thức tính các đại lượng đặc trưng của dao động thông qua đồ thị
Lời giải chi tiết:
a) Biên độ dao động A=0,2 cm
Chu kì T=0,4 s
Tần số \(f = \frac{1}{T} = \frac{1}{{0,4}} = 2,5Hz\)
Tần số góc của dao động \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,4}} = 5\pi rad/s\)
b) Li độ của vật dao động tại các thời điểm t1, t2, t3 ứng với các điểm A, B, C trên đường đồ thị li độ – thời gian lần lượt là x1=-0,1 cm, x2= -0,2 cm, x3= 0 cm.
c) Vì gốc thời gian trùng với vị trí cân bằng nên li độ cũng chính là độ dịch chuyển từ vị trí cân bằng đến vị trí của vật tại các điểm A, B, C.
Câu hỏi tr 15 CH
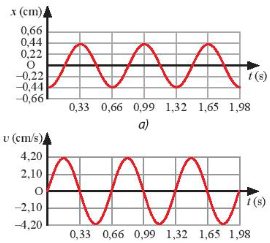
Quan sát Hình 2.3a và 2.3b, hãy xác định:
a) Hình dạng đồ thị vận tốc – thời gian của vật.
b) Chu kì của vận tốc của vật.
c) Mối liên hệ giữa tốc độ cực đại và biên độ của vật.
d) Độ lệch pha của vận tốc so với li độ của vật.
Phương pháp giải:
Áp dụng kiến thức dã học về dao động
Lời giải chi tiết:
a) Hình dạng đồ thị vận tốc – thời gian của vật là dạng hình sin.
b) Chu kì của vận tốc của vật T=0,66 s.
c) Mối liên hệ giữa tốc độ cực đại và biên độ của vật: khi vận tốc cực đại thì biên độ cực tiểu và ngược lại.
d) Độ lệch pha của vận tốc so với li độ của vật là \(\frac{\pi }{2}\)
Câu hỏi tr 16 LT
Một vật dao động điều hòa với biên độ 10 cm và chu kì 2s. Chọn gốc thời gian là khi vật qua vị trí cân bằng theo chiều dương. Xác định vận tốc của vật vào thời điểm đó.
Phương pháp giải:
Áp dụng kiến thức dã học về dao động \(v = \omega A\)
Lời giải chi tiết:
Vận tốc của vật vào thời điểm đó là: \(v = \omega A = \frac{{2\pi }}{T}.A = \frac{{2\pi }}{2}.10 = 10\pi cm/s\)
Câu hỏi tr 17 CH 1
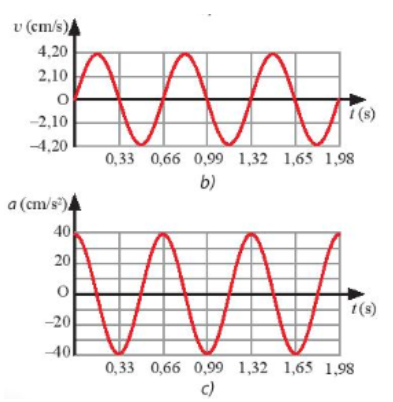
Quan sát Hình 2.3a và 2.3c, hãy xác định:
a) Hình dạng đồ thị gia tốc – thời gian của vật.
b) Chu kì của gia tốc của vật.
c) Mối liên hệ giữa gia tốc cực đại và biên độ của vật.
d) Độ lệch pha của gia tốc so với li độ của vật.
Phương pháp giải:
Áp dụng kiến thức đã học, quan sát đồ thị
Lời giải chi tiết:
a) Hình dạng đồ thị gia tốc – thời gian của vật là dạng hình sin.
b) Chu kì của gia tốc của vật là T=0,66 s.
c) Mối liên hệ giữa gia tốc cực đại và biên độ của vật là khi gia tốc đạt giá trị cực đại khi ở vị trí biên và cực tiểu khi ở vị trí cân bằng.
d) Độ lệch pha của gia tốc so với li độ của vật là π.
Câu hỏi tr 17 CH 2
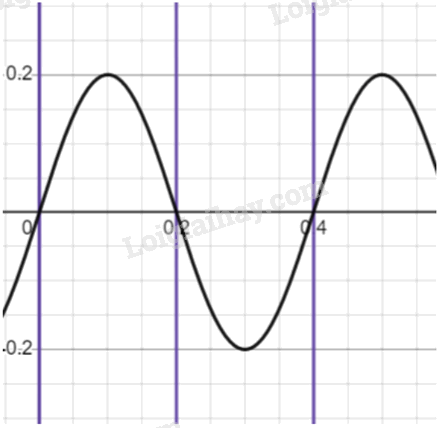
Hãy vẽ phác đồ thị lực tác dụng - thời gian của vật dao động điều hoà có đồ thị li độ – thời gian như Hình 2.2.
Phương pháp giải:
Áp dụng kiến thức đã học, quan sát đồ thị
Lời giải chi tiết:
Phương trình dao động của vật: x=0.2.cos(5π.x−\(\frac{\pi }{2}\))
Phương trình lực tác dụng của vật là F=−m.(5π)2.0.2.cos(5πx−\(\frac{\pi }{2}\))
Đường màu đen là phương trình dao động, đường màu tím là lực tác dụng.
Câu hỏi tr 18 LT
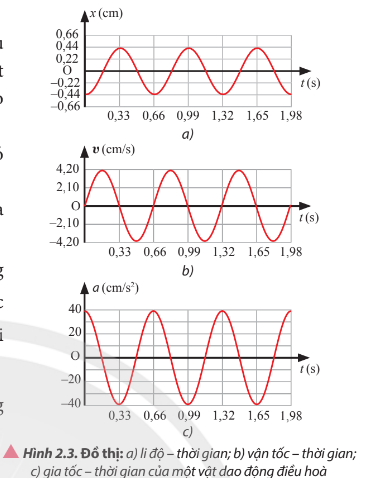
Dựa vào các đồ thị trong Hình 2.3:
a) Viết phương trình li độ, vận tốc và gia tốc của vật dao động điều hòa.
b) Mô tả định tính tính chất của li độ, vận tốc và gia tốc của vật tại các thười điểm 0,33 s; 0,495s và 0,66 s
c) Dựa vào các phương trình được xây dựng ở câu a để kiểm chứng lại mô tả định tính ở câu b
Phương pháp giải:
Áp dụng kiến thức đã học về phương trình dao động điều hòa: \(x = A\cos (\omega t + \varphi )\)
Lời giải chi tiết:
Biên độ dao động: A = 0,44 cm
Tốc độ cực đại: vmax = 4,2 cm/s
Gia tốc cực đại: amax = 40 cm/s2
Chu kì của gia tốc của vật: T = 0,66 s.
Tốc độ góc: \(\omega = \frac{{2\pi }}{T} = \frac{{100}}{{33}}\pi (rad/s)\)
a) Tại thời điểm ban đầu vật đi từ biên âm tiến về VTCB nên pha ban đầu φ0 = π(rad)
Khi đó, phương trình li độ có dạng:
x = Acos(ωt+φ0) = 0,44cos(\(\frac{{100\pi }}{{33}}\)t+π) (cm)
Phương trình vận tốc có dạng:
v = ωAcos(ωt+φ0+\(\frac{\pi }{2}\)) = 4,2cos(\(\frac{{100\pi }}{{33}}\)t+\(\frac{{3\pi }}{2}\)) (cm/s)
Phương trình gia tốc có dạng:
a = −ω2Acos(ωt+φ0) = −40cos(\(\frac{{100\pi }}{{33}}\)t+π) (cm/s2)
b)
Từ đồ thị có thể thấy:
t= 0,33s: x=0,44 cm; v=0 cm/s; a=-40 cm/s2
t= 0,495s: x=0 cm; v=-4,2 cm/s; a=0 cm/s2
t= 0,66s: x=-0,44 cm; v=0 cm/s; a=40 cm/s2
c) Nghiệm lại với các phương trình.
- Tại thời điểm t = 0,5 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).0,5+π) = −0,02 (cm)
v =4,2cos(\(\frac{{100\pi }}{{33}}\).0,5+3π2) = −4,19 (cm/s)
a =−40cos(\(\frac{{100\pi }}{{33}}\).0,5+π) = 1,9 (cm/s2)
- Tại thời điểm t = 0,75 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).0,75+π) = −0,29 (cm)
v = 4,2cos(\(\frac{{100\pi }}{{33}}\).0,75+\(\frac{{3\pi }}{2}\)) = 3,17 (cm/s)
a = −40cos(\(\frac{{100\pi }}{{33}}\).0,75+π) = 26,2 (cm/s2)
- Tại thời điểm t = 1 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).1+π) = 0,438 (cm)
v = 4,2cos(\(\frac{{100\pi }}{{33}}\).1+3π2) = −0,4 (cm/s)
a = −40cos(\(\frac{{100\pi }}{{33}}\).1+π) = −39,8 (cm/s2)
Câu hỏi tr 19 CH
Nhận xét về độ lệch pha giữa gia tốc và vận tốc của vật dao động.
Phương pháp giải:
Sử dụng kiến thức đã học
Lời giải chi tiết:
Độ lệch pha giữa gia tốc và vận tốc là \(\frac{\pi }{2}\)
Câu hỏi tr 19 LT
Một máy cơ khí khi hoạt động sẽ tạo ra những dao động được xem gần đúng là dao động điều hoà với phương trình li độ có dạng:
x=2cos(180πt) (mm)
a) Hãy xác định biên độ, chu kì, tần số và tần số góc của dao động.
b) Viết phương trình vận tốc và gia tốc của vật dao động.
Phương pháp giải:
Áp dụng kiến thức đã học về phương trình dao động điều hòa: \(x = A\cos (\omega t + \varphi )\)
Lời giải chi tiết:
a) Biên độ A= 2 mm
Tần số góc ω = 180π (rad/s)
Chu kì \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{180\pi }} = \frac{1}{{90}}s\)
Tần số \(f = \frac{1}{T} = 90Hz\)
b) Phương trình vận tốc là:
v = −180π.2sin(180πt) = 360πsin(180πt) (mm/s)
Phương trình gia tốc là: a = −(180π)2.2cos(180πt) (mm/s2)
Câu hỏi tr 19 VD
Tìm hiểu và trình bày ngắn gọn nguyên tắc hoạt động của thiết bị đo khối lượng của các phi hành gia trên tàu vũ trụ.
Phương pháp giải:
Áp dụng kiến thức đã học
Lời giải chi tiết:
Ở ngoài vũ trụ, không trọng lượng nên không thể dùng cân hay lực kế để xác đinh khối lượng.
Khi đó, người ta dùng một dụng cụ đo khối lượng là một chiếc ghế lắp vào đầu một lò xo (đầu kia của lò xo gắn vào một điểm trên tàu). Nhà du hành ngồi vào ghế và thắt dây buộc mình vào ghế, cho ghế dao động và đo chu kì dao động T của ghế bằng một đồng hồ hiện số đặt trước mặt mình.
Bài tập Bài 1
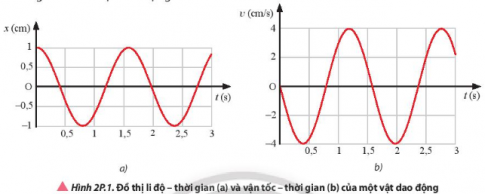
Một vật dao động điều hoà có đồ thị li độ – thời gian và vận tốc – thời gian như Hình 2P.1. Hãy viết phương trình li độ và phương trình vận tốc của dao động này. Từ đó suy ra phương trình gia tốc của vật dao động.
Phương pháp giải:
Áp dụng kiến thức đã học
Lời giải chi tiết:
Từ đồ thị ta xác định được A = 1cm
Ta có: vmax = ωA⇒ω = 4 (rad/s)
Phương trình li độ của dao động: x = cos(4t) (cm)
Phương trình vận tốc của dao động: v = 4cos(4t+\(\frac{\pi }{2}\)) (cm/s)
Phương trình gia tốc của vật dao động: a = 16cos(4t) (m/s2)
Bài tập Bài 2
Một chất điểm dao động điều hoà với biên độ 4 cm, tần số 1 Hz. Tại thời điểm ban đầu, vật ở vị trí biên âm. Hãy xác định vận tốc và gia tốc của vật tại thời điểm t = 1s.
Phương pháp giải:
Áp dụng kiến thức đã học
Lời giải chi tiết:
Ta có tần số f = 1 Hz \( \Rightarrow \omega = 2\pi f = 2\pi (rad/s)\)
Pha ban đầu của dao động là: φ0 = π
Phương trình dao động của vật là: x = 4cos(2πt+π) (cm)
Vận tốc của vật tại thời điểm t=1s là: v = −ωAsin(ωt+φ0) = −2π.4.sin(2π+π) = 0
Gia tốc của vật tại thời điểm t=1s là: a = −ω2.4cos(2πt+π) = −(2π)2.4cos(2π+π) = 16π2 (cm/s2)
Bài tập Bài 3
Một vật dao động điều hoà có đồ thị gia tốc theo thời gian được thể hiện trong Hình 2P.2.
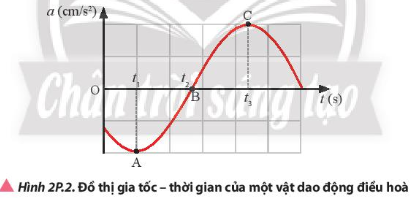
Xác định vị trí, vận tốc và gia tốc của vật tại các thời điểm t1, t2, t3 tương ứng với các điểm A, B và C trên đường đồ thị a(t)
Phương pháp giải:
Áp dụng kiến thức đã học
Lời giải chi tiết:
Vị trí A có gia tốc a1 = -ω2A nên vật ở vị trí biên dương, khi đó vận tốc v = 0
Vị trí B có gia tốc a2 = 0 nên vật ở vị trí cân bằng có vận tốc bằng v=ωA
Vị trí C có gia tốc a3 = ω2A > 0 nên vật ở vị trí biên âm có vận tốc bằng 0
Luyện Bài Tập Trắc nghiệm Lí 11 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Lý thuyết Năng lượng điện. Công suất điện - Vật Lí 11 Chân trời sáng tạo
- Lý thuyết Nguồn điện - Vật Lí 11 Chân trời sáng tạo
- Lý thuyết Điện trở. Định luật Ohm - Vật Lí 11 Chân trời sáng tạo
- Lý thuyết Năng lượng và ứng dụng của tụ điện - Vật Lí 11 Chân trời sáng tạo
- Lý thuyết Dòng điện. Cường độ dòng điện - Vật Lí 11 Chân trời sáng tạo
- Lý thuyết Năng lượng điện. Công suất điện - Vật Lí 11 Chân trời sáng tạo
- Lý thuyết Nguồn điện - Vật Lí 11 Chân trời sáng tạo
- Lý thuyết Điện trở. Định luật Ohm - Vật Lí 11 Chân trời sáng tạo
- Lý thuyết Năng lượng và ứng dụng của tụ điện - Vật Lí 11 Chân trời sáng tạo
- Lý thuyết Dòng điện. Cường độ dòng điện - Vật Lí 11 Chân trời sáng tạo












