Bài 32. Lực hướng tâm và gia tốc hướng tâm trang 123, 124, 125, 126 Vật Lí 10 Kết nối tri thức
Tại sao Trái Đất chuyển động quanh Mặt Trời? Tại sao trên những đoạn đường vòng thường phải hạn chế tốc độ của xe và mặt đường thường phải nghiêng về phía tâm. Lực nào sau đây làm cái tẩy chuyển động tròn. Nếu cái tẩy đang chuyển động mà ta buông tay ra thì. Lực nào duy trì chuyển động tròn của Trái Đất xung quanh Mặt Trời.
Video hướng dẫn giải
Câu hỏi tr 123 MĐ
|
Tại sao Trái Đất chuyển động quanh Mặt Trời? Tại sao trên những đoạn đường vòng thường phải hạn chế tốc độ của xe và mặt đường thường phải nghiêng về phía tâm?
|
Phương pháp giải:
Vận dụng các kiến thức đã học
Lời giải chi tiết:
+ Trái Đất chuyển động quanh Mặt Trời là nhờ sức kéo từ trọng lực của Mặt Trời.
+ Trên những đoạn đường vòng thường phải hạn chế tốc độ của xe và mặt đường thường phải nghiêng về phía tâm vì như vậy thì phương tiện tham gia giao thông sẽ giữ được cân bằng và lực li tâm khi rẽ.
Câu hỏi tr 123 CH 1
|
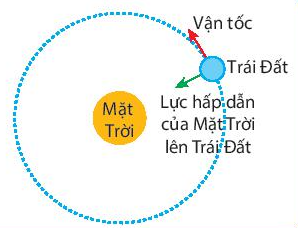
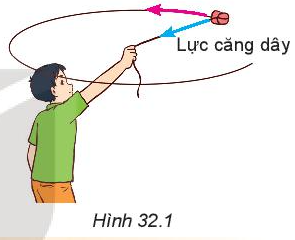
1. Lực nào sau đây làm cái tẩy chuyển động tròn? - Trọng lực tác dụng lên cái tẩy. - Lực cản của không khí. - Lực căng dây hướng vào tâm quỹ đạo của cái tẩy. 2. Nếu cái tẩy đang chuyển động mà ta buông tay ra thì: - Cái tẩy tiếp tục chuyển động tròn. - Cái tẩy sẽ rơi xuống đất theo phương thẳng đứng. - Cái tẩy văng theo phương tiếp tuyến với quỹ đạo theo hướng vận tốc tại điểm đó. 3. Lực nào duy trì chuyển động tròn của Trái Đất xung quanh Mặt Trời? |
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
1.
Lực làm cái tẩy chuyển động tròn là lực căng dây hướng vào tâm quỹ đạo của cái tẩy.
2.
Vận tốc của cái tẩy vuông góc với phương tiếp tuyến của lực căng nên nếu buông tay thì cái tẩy sẽ văng theo phương tiếp tuyến với quỹ đạo theo hướng vận tốc tại thời điểm đó.
3.
Lực duy trì chuyển động tròn của Trái Đất xung quanh Mặt Trời là lực hướng tâm.
Câu hỏi tr 123 CH 2
|
Tìm thêm ví dụ về lực hướng tâm |
Phương pháp giải:
Liên hệ thực tế
Lời giải chi tiết:
+ Cánh quạt đang quay
+ Kim đồng hồ quay
+ Trái Đất quay xung quanh Mặt Trời
Câu hỏi tr 124
|
1. Tính gia tốc hướng tâm của một vệ tinh nhân tạo chuyển động tròn đều quanh Trái Đất với bán kính quỹ đạo là 7 000 km và tốc độ 7,57 km/s. 2. Tính gia tốc hướng tâm của Mặt Trăng trong chuyển động quay quanh Trái Đất (coi Mặt Trăng chuyển động tròn đều quanh Trái Đất). Biết khoảng cách từ Mặt Trăng đến tâm Trái Đất là 3,84.108 m và chu kì quay là 27,2 ngày. 3. Kim phút của một chiếc đồng hồ dài 8 cm. Tính gia tốc hướng tâm của đầu kim. |
Phương pháp giải:
Biểu thức tính gia tốc hướng tâm:
\({a_{ht}} = \frac{{{v^2}}}{r}\)
Trong đó:
+ aht : gia tốc hướng tâm (m/s2 )
+ v: tốc độ chuyển động của vật (m/s)
+ r: bán kính quỹ đạo của chuyển động (m)
Lời giải chi tiết:
1.
Đổi 7 000 km = 7.106 m; 7,57 km/s = 7570 m/s
Gia tốc hướng tâm của vệ tinh nhân tạo là:
\({a_{ht}} = \frac{{{v^2}}}{r} = \frac{{{{7570}^2}}}{{{{7.10}^6}}} \approx 8,19(m/{s^2})\)
2.
Đổi T = 27,2 ngày = 2 350 080 s
Gia tốc hướng tâm của Mặt trăng chuyển động quay quanh Trái Đất là:
\({a_{ht}} = {\omega ^2}.r = {\left( {\frac{{2\pi }}{T}} \right)^2}.r = {\left( {\frac{{2\pi }}{{2350080}}} \right)^2}.3,{84.10^8} \approx 2,{74.10^{ - 3}}(m/{s^2})\)
3.
Kim phút quay hết 1 vòng đồng hồ là 1 giờ
Ta có:
+ Chu kì T = 1 giờ = 3600 s
+ Bán kính r = 8 cm = 0,08 m
Gia tốc hướng tâm của đầu kim phút là:
\({a_{ht}} = {\omega ^2}.r = {\left( {\frac{{2\pi }}{T}} \right)^2}.r = {\left( {\frac{{2\pi }}{{3600}}} \right)^2}.0,08 \approx 2,{4.10^{ - 7}}(m/{s^2})\)
Câu hỏi tr 125 HĐ 1
|
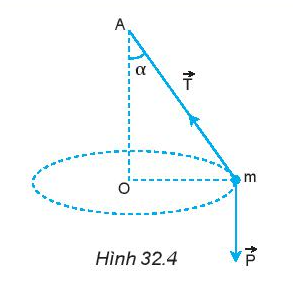
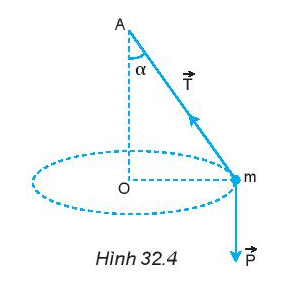
Vẽ hợp lực của lực căng dây \(\overrightarrow T \)và trọng lực \(\overrightarrow P \), từ đó xác định lực hướng tâm trong Hình 32.4
|
Phương pháp giải:
Vận dụng các kiến thức đã học
Lời giải chi tiết:
Hợp lực của lực căng dây \(\overrightarrow T \)và trọng lực \(\overrightarrow P \):
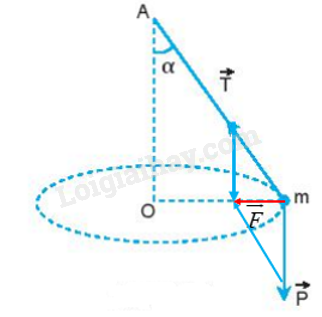
Lực hướng tâm chính là hợp lực của \(\overrightarrow T \)và \(\overrightarrow P \)
Câu hỏi tr 125 CH
|
1. Trong trường hợp ở Hình 32.4, dây dài 0,75 m.
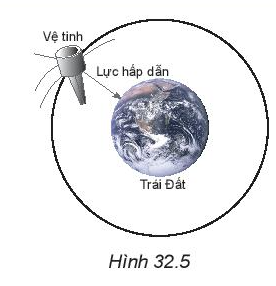
a) Bạn A nói rằng: “Tốc độ quay càng lớn thì góc lệch của dây so với phương thẳng đứng cũng càng lớn”. Hãy chứng minh điều đó. b) Tính tần số quay để dây lệch góc α = 600 so với phương thẳng đứng, lấy g = 9,8 m/s2 . 2. Hình 32.5 mô tả một vệ tinh nhân tạo quay quanh Trái Đất.
a) Lực nào là lực hướng tâm? b) Nếu vệ tinh trên là vệ tinh địa tĩnh (nằm trong mặt phẳng xích đạo của Trái Đất và có tốc độ góc bằng tốc độ góc tự quay của Trái Đất quanh trục của nó). Hãy tìm gia tốc hướng tâm của vệ tinh. Cho gần đúng bán kính Trái Đất là 6 400 km và độ cao của vệ tinh so với mặt đất bằng 35 780 km. |
Phương pháp giải:
1.
+ Biểu thức tính tốc độ góc: \(\omega = \frac{{\Delta \alpha }}{{\Delta t}}\)
Trong đó: Δα là góc quay của chất điểm trong thời gian Δt
2.
Quan sát hình vẽ
- Biểu thức tính gia tốc hướng tâm: \({a_{ht}} = {\omega ^2}.r\)
Trong đó:
+ aht : gia tốc hướng tâm (m/s2 )
+ r: khoảng cách từ chất điểm tới tâm Trái Đất (m)
+ \(\omega \): tốc độ góc (rad/s)
- Mối liên hệ giữa chu kì và tốc độ góc: \(T = \frac{{2\pi }}{\omega }\) (s)
Trái Đất quay một vòng xung quanh trục của nó mất 1 ngày
Lời giải chi tiết:
1.
a) Trong một khoảng thời gian ngắn, coi như thời gian không đổi, ta có tốc độ tỉ lệ thuận với góc quay
=> Tốc độ quay càng lớn thì góc lệch của dây so với phương thẳng đứng cũng càng lớn
b)

Bán kính của vật là: r = l.sinα = 0,75.sin600 = 0,65 (m)
Ta có:
\(\begin{array}{l}{F_{ht}} = P.\tan \alpha \Rightarrow m.{a_{ht}} = m.g.\tan \alpha \\ \Leftrightarrow {a_{ht}} = g.\tan \alpha \Leftrightarrow {\omega ^2}.r = g.\tan \alpha \\ \Rightarrow \omega = \sqrt {\frac{{g.\tan \alpha }}{r}} = \sqrt {\frac{{9,8.\tan {{60}^0}}}{{0,65}}} \approx 5,11(rad/s)\end{array}\)
2.
Do Trái Đất quay một vòng xung quanh trục của nó mất 1 ngày nên chu kì của Trái Đất là T = 24 giờ = 24.86400 s
Khoảng cách từ vệ tinh đến tâm Trái Đất: r = 6400 + 35 780 = 42 180 km = 4218.104 m
Gia tốc hướng tâm của vệ tinh là:
\({a_{ht}} = {\omega ^2}.r = {\left( {\frac{{2\pi }}{T}} \right)^2}.r = {\left( {\frac{{2\pi }}{{24.86400}}} \right)^2}{.4218.10^4} \approx 3,{87.10^{ - 4}}(m/{s^2})\)
Câu hỏi tr 125 HĐ 2
|
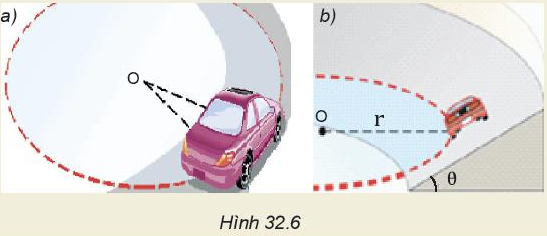
Hình 32.6 mô tả ô tô chuyển động trên quỹ đạo tròn trong hai trường hợp: mặt đường nằm ngang (Hình 32.6a) và mặt đường nghiêng góc θ (Hình 32.6b). Hãy thảo luận và cho biết:
a) Lực nào là lực hướng tâm trong mỗi trường hợp. b) Lí do để ở các đoạn đường cong phải làm mặt đường nghiêng về phía tâm. c) Tại sao các phương tiện giao thông phải giảm tốc khi vào các cung đường tròn? |
Phương pháp giải:
Vận dụng kiến thức đã học và quan sát hình vẽ
Lời giải chi tiết:
a)
- Hình 32.6a: Lực ma sát đóng vai trò là lực hướng tâm.
- Hình 32.6b: Các thành phần theo phương nằm ngang của phản lực N và của lực ma sát đóng vai trò là lực hướng tâm.
b) Vì để đảm bảo sự di chuyển và an toàn của người và phương tiện. Khi xe chạy ở các đoạn đường cong, lực ma sát giữa các bánh xe và mặt đường không đủ để tạo lực hướng tâm. Do phải tồn tại lực hướng tâm để xe có thể thực hiện chuyển động tròn nên mặt đường phải được thiết kế nghiêng một góc so với phương ngang để hợp lực hướng vào tâm đường tròn và đóng vai trò lực hướng tâm, bảo đảm cho xe chạy vòng theo quỹ đạo tròn.
c) Các phương tiện giao thông phải giảm tốc khi vào các cung đường tròn vì để đảm bảo sự an toàn cho người và phương tiện. Nếu các phương tiện giao thông chuyển động với tốc độ lớn, lực hướng tâm không đủ để giữ cho chúng chuyển động tròn theo quỹ đạo, khi đó xe sẽ bị văng ra khỏi quỹ đạo.
Luyện Bài Tập Trắc nghiệm Lí 10 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Lí thuyết Bài 34. Khối lượng riêng. Áp suất chất lỏng - Vật lí 10
- Lí thuyết Bài 33. Biến dạng của vật rắn - Vật lí 10
- Lí thuyết Bài 32. Lực hướng tâm và gia tốc hướng tâm - Vật lí 10
- Lí thuyết Bài 31. Động học của chuyển động tròn đều - Vật lí 10
- Lí thuyết Bài 29. Định luật bảo toàn động lượng - Vật lí 10
- Lí thuyết Bài 34. Khối lượng riêng. Áp suất chất lỏng - Vật lí 10
- Lí thuyết Bài 33. Biến dạng của vật rắn - Vật lí 10
- Lí thuyết Bài 32. Lực hướng tâm và gia tốc hướng tâm - Vật lí 10
- Lí thuyết Bài 31. Động học của chuyển động tròn đều - Vật lí 10
- Lí thuyết Bài 29. Định luật bảo toàn động lượng - Vật lí 10













Danh sách bình luận