Bài 31. Động học của chuyển động tròn đều trang 120, 121, 122 Vật Lí 10 Kết nối tri thức
Khi xe mô tô đua vào khúc cua thì có những bộ phận nào của xe chuyển động tròn. Chứng minh rằng một radian là góc ở tâm chắn cung có độ dài bằng bán kính đường tròn. Tính quãng đường đi được khi vật chuyển động tròn có độ dịch chuyển góc 1 rad, biết bán kính đường tròn là 2 m.
Video hướng dẫn giải
Câu hỏi tr 120 MĐ
|
Khi xe mô tô đua vào khúc cua thì có những bộ phận nào của xe chuyển động tròn?
|
Phương pháp giải:
Quan sát hình và vận dụng thực tế
Lời giải chi tiết:
Khi xe mô tô đua vào khúc cua thì bộ phận của xe chuyển động tròn là: bánh xe.
Câu hỏi tr 120 CH
|
1. Chứng minh rằng một radian là góc ở tâm chắn cung có độ dài bằng bán kính đường tròn. 2. Tính quãng đường đi được khi vật chuyển động tròn có độ dịch chuyển góc 1 rad, biết bán kính đường tròn là 2 m. 3. Xét chuyển động của kim giờ đồng hồ. Tìm độ dịch chuyển góc của nó (theo độ và radian): a) Trong mỗi giờ. b) Trong khoảng thời gian từ 12 h đến 15 h 30 min. |
Phương pháp giải:
1.
Mối quan hệ giữa độ dài cung với góc chắn tâm và bán kính đường tròn: \(\theta = \frac{s}{r}\)
Trong đó:
+ \(\theta \): góc chắn tâm (rad)
+ s: độ dài cung (m)
+ r: bán kính đường tròn (m).
2.
Mối quan hệ giữa độ dài cung với góc chắn tâm và bán kính đường tròn: \(\theta = \frac{s}{r}\)
Trong đó:
+ \(\theta \): góc chắn tâm (độ dịch chuyển góc) (rad)
+ s: độ dài cung (m)
+ r: bán kính đường tròn (m).
3.
- Mối quan hệ giữa độ dài cung với góc chắn tâm và bán kính đường tròn: \(\theta = \frac{s}{r}\)
Trong đó:
+ \(\theta \): góc chắn tâm (độ dịch chuyển góc) (rad)
+ s: độ dài cung (m)
+ r: bán kính đường tròn (m).
- 1. Π = 1800
Lời giải chi tiết:
1.
Ta có \(\theta \) = 1 rad
\( \Rightarrow \theta = \frac{s}{r} = 1 \Rightarrow s = r\)
Vậy góc chắn tâm bằng 1 radian thì độ dài cung bằng bán kính đường tròn.
2.
Ta có \(\theta \) = 1 rad
\( \Rightarrow \theta = \frac{s}{r} = 1 \Rightarrow s = r = 2(m)\)
3.
a) Ta có 1 vòng tròn tương ứng là 2π rad
=> 1 giờ vật quay được góc của đồng hồ
=> Độ dịch chuyển góc của kim giờ trong 1 giờ đồng hồ là \(\frac{{2\pi }}{{12}} = \frac{\pi }{6}\)
Đổi \(\frac{\pi }{6} = {\left( {\frac{\pi }{6}.\frac{{180}}{\pi }} \right)^0} = {30^0}\)
b)
Từ 12 h đến 15 h 30 min, độ dịch chuyển thời gian là 3 h 30 min = 3,5 giờ
Ta có 1 giờ vật quay được góc của đồng hồ
=> 3,5 h vật quay được \(3,5.\frac{1}{{12}} = \frac{7}{{24}}\) góc đồng hồ
=> Độ dịch chuyển góc của kim giờ trong 3,5 h đồng hồ là \(2\pi .\frac{7}{{24}} = \frac{{7\pi }}{{12}}\)
Đổi \(\frac{{7\pi }}{{12}} = {\left( {\frac{{7\pi }}{{12}}.\frac{{180}}{\pi }} \right)^0} = {105^0}\)
Câu hỏi tr 121 CH 1
|
Dựa vào việc quan sát chuyển động của kim giây trong đồng hồ có kim trôi để: 1. So sánh tốc độ của các điểm khác nhau trên kim 2. So sánh độ dịch chuyển góc trong cùng khoảng thời gian của các điểm khác nhau trên kim. |
Phương pháp giải:
Quan sát chuyển động của các kim trên đồng hồ
Lời giải chi tiết:
1.
Ta thấy tốc độ của các điểm khi kim giây chuyển động là như nhau trên đường tròn
2.
Độ dịch chuyển góc trong cùng khoảng thời gian của các điểm khác nhau trên kim là như nhau.
Câu hỏi tr 121 CH 2
|
Câu 1: Hãy tính tốc độ góc của kim giờ và kim phút của đồng hồ. Câu 2: Roto trong một tổ máy thủy điện Hòa Bình quay 125 vòng mỗi phút. Hãy tính tốc độ góc của roto này theo đơn vị rad/s.
|
Phương pháp giải:
Mối liên hệ giữa chu kì và tốc độ góc trong chuyển động tròn đều là: \(\omega = \frac{{2\pi }}{T}\)
Trong đó:
+ T là chu kì (s)
+ \(\omega \): tốc độ góc (rad/s)
Lời giải chi tiết:
1.
Chu kì quay của kim giờ là 12 giờ = 43200 s
Chu kì quay của kim phút là 60 phút = 3600 s
Tốc độ góc của kim giờ là: \({\omega _h} = \frac{{2\pi }}{{{T_h}}} = \frac{{2\pi }}{{43200}} \approx {1,5.10^{ - 4}}(rad/s)\)
Tốc độ góc của kim phút là: \({\omega _{phút}} = \frac{{2\pi }}{{{T_{phút}}}} = \frac{{2\pi }}{{3600}} \approx 1,{75.10^{ - 3}}(rad/s)\)
2.
Ta có f = 125 vòng/phút = vòng/s
Tốc độ góc của roto là: \(\omega = 2\pi f = 2\pi .\frac{{25}}{{12}} \approx 13,1(rad/s)\)
Câu hỏi tr 121 CH 3
| 1. Biết chiều dài kim phút và kim giây của một chiếc đồng hồ lần lượt là 4 cm và 5 cm. Hãy tính:
a) Tỉ số chu kì quay của hai kim. b) Tỉ số tốc độ của đầu kim phút và đầu kim giây. 2. Xét một điểm nằm trên đường xích đạo trong chuyển động tự quay của Trái Đất. Biết bán kính Trái Đất tại xích đạo là 6 400 km. Hãy tính:
a) Chu kì chuyển động của điểm đó. b) Tốc độ và tốc độ góc của điểm đó. |
Phương pháp giải:
Trái Đất tự quay quanh trục của nó 1 vòng hết 24 giờ
- Chu kì quay trong chuyển động tròn đều là: \(T = \frac{{2\pi }}{\omega }\)
Trong đó:
+ T là chu kì (s)
+ \(\omega \): tốc độ góc (rad/s)
- Mối liên hệ giữa tốc độ và tốc độ góc trong chuyển động tròn đều là: \(v = \omega .r\)
Lời giải chi tiết:
1.
a) Chu kì là khoảng thời gian để vật quay hết một vòng tròn
+ Chu kì quay của kim phút là 60 phút = 3600 giây
+ Chu kì quay của kim giây là 60 giây
b) Ta có: \(v = \omega .r = \frac{{2\pi }}{T}.r\)
\(\begin{array}{l}{v_{phút}} = \frac{{2\pi }}{{{T_{phút}}}}.{r_{phút}}\\{v_{giây}} = \frac{{2\pi }}{{{T_{giây}}}}.{r_{giây}}\end{array}\)
\( \Rightarrow \frac{{{v_{phút}}}}{{{v_{giây}}}} = \frac{{{r_{phút}}}}{{{r_{giây}}}}.\frac{{{T_{giây}}}}{{{T_{phút}}}} = \frac{4}{5}.\frac{{60}}{{3600}} = \frac{1}{{75}}\)
2.
a) Trái Đất tự quay quanh trục của nó 1 vòng hết 24 giờ
=> Chu kì chuyển động của một điểm trong chuyển động tự quay của Trái Đất là 24 giờ.
b) Đổi 24 giờ = 86400 s; 6400 km = 6,4.106 m.
Tốc độ góc của điểm đó là: \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{86400}} \approx {7.10^{ - 5}}(rad/s)\)
Tốc độ của điểm đó là:
\(v = \omega .r = {7.10^{ - 5}}.6,{4.10^6} = 465,4(m/s)\)
Câu hỏi tr 122
|
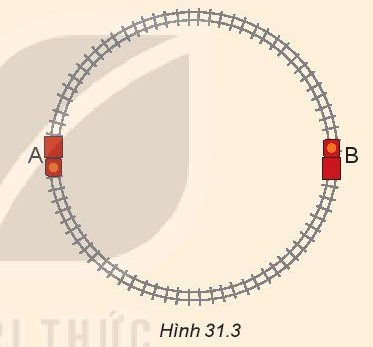
1. Phân biệt tốc độ và độ lớn của vận tốc trong chuyển động tròn đều. 2. Nêu mối quan hệ giữa tốc độ v, chu kì T và bán kính r của một vật chuyển động tròn đều 3. Một xe đồ chơi chạy với tốc độ không đổi 0,2 m/s trên một đường ray tròn tâm O, đường kính AB theo chiều kim đồng hồ. (Hình 31.3) Xác định sự thay đổi vận tốc khi xe đi từ A đến B
|
Phương pháp giải:
1.
Vận dụng lí thuyết trong sách giáo khoa trang 121-122
2.
- Chu kì quay trong chuyển động tròn đều là: \(T = \frac{{2\pi }}{\omega }\)
Trong đó:
+ T là chu kì (s)
+ \(\omega \): tốc độ góc (rad/s)
3.
Trong chuyển động tròn đều, vận tốc đều có độ lớn không đổi
Lời giải chi tiết:
1.
+ Vận tốc có độ lớn không đổi nhưng hướng luôn thay đổi ( vận tốc là đại lượng vecto)
+ Tốc độ có độ lớn và hướng không đổi (tốc độ là đại lượng vô hướng).
2.
- Mối liên hệ giữa tốc độ và tốc độ góc trong chuyển động tròn đều là: \(v = \omega .r\)
=> v tỉ lệ thuận với r.
- Ta có: \(v = \omega .r = \frac{{2\pi }}{T}.r\)
Trong chuyển động tròn đều, v tỉ lệ nghịch với T.
3.
Khi xe đi từ A đến B thì vận tốc của xe không đổi nhưng hướng thay đổi, vận tốc của xe là 0,2 m/s.
Luyện Bài Tập Trắc nghiệm Lí 10 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Lí thuyết Bài 34. Khối lượng riêng. Áp suất chất lỏng - Vật lí 10
- Lí thuyết Bài 33. Biến dạng của vật rắn - Vật lí 10
- Lí thuyết Bài 32. Lực hướng tâm và gia tốc hướng tâm - Vật lí 10
- Lí thuyết Bài 31. Động học của chuyển động tròn đều - Vật lí 10
- Lí thuyết Bài 29. Định luật bảo toàn động lượng - Vật lí 10
- Lí thuyết Bài 34. Khối lượng riêng. Áp suất chất lỏng - Vật lí 10
- Lí thuyết Bài 33. Biến dạng của vật rắn - Vật lí 10
- Lí thuyết Bài 32. Lực hướng tâm và gia tốc hướng tâm - Vật lí 10
- Lí thuyết Bài 31. Động học của chuyển động tròn đều - Vật lí 10
- Lí thuyết Bài 29. Định luật bảo toàn động lượng - Vật lí 10














Danh sách bình luận