Giải bài 3.13 trang 37 sách bài tập toán 8 - Kết nối tri thức với cuộc sống

Chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu hai đáy của nó.

Đề bài

Chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu hai đáy của nó.

Phương pháp giải - Xem chi tiết

+ Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Hình bình hành có các cạnh đối bằng nhau.

+ Sử dụng kiến thức về dấu hiệu nhận biết hình bình hành để chứng minh: Tứ giác có các cạnh đối song song là hình bình hành.

Lời giải chi tiết

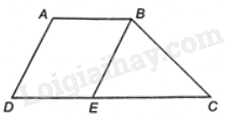
Giả sử hình thang ABCD có hai đáy là AB, CD. Giả sử \(AB < DC\). Qua B kẻ đường thẳng song song với AD cắt DC tại E.

Tứ giác ABED có: AB//DE, AD//EB nên tứ giác ABED là hình bình hành. Do đó, \(AB = DE,AD = EB\)

Vì \(AB < DC\) nên E nằm giữa D và C.

Do đó, \(EC = DC - DE = DC - AB\) (1)

Tam giác BEC có: \(BE + BC > EC\) (bất đẳng thức trong tam giác)

Mà \(AD = EB\) nên \(AD + BC > EC\) (2)

Từ (1) và (2) ta có: \(AD + BC > DC - AB\)

Bình luận

Chia sẻ

Bình chọn:

4 trên 14 phiếu

Bài tiếp theo

Giải bài 3.14 trang 37 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
Cho hình bình hành ABCD với góc A tù. Dựng bên ngoài hình bình hành đó các tam giác đều ABE và DAF. Chứng minh rằng tam giác CEF là tam giác đều.
Giải bài 3.15 trang 37 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
Chứng minh rằng nếu hai góc kề của mỗi cạnh của một tứ giác đều là hai góc bù nhau thì tứ giác đó là một hình bình hành.
Giải bài 3.16 trang 37 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
Cho hình thang ABCD với hai đáy AB, CD. Gọi K là trung điểm của BC. Lấy điểm A’, D’ sao cho K và trung điểm của AA’ và DD’. Hỏi tứ giác AD’A’D là hình gì? Vì sao?
Giải bài 3.17 trang 37 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
Cho hai điểm phân biệt A, B nằm bên trong góc xOy (không bẹt). Tìm điểm D thuộc tia Ox, điểm E thuộc tia Oy sao cho ADBE là một hình bình hành.
Giải bài 3.18 trang 37 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
Cho hình bình hành ABCD. Lấy các điểm E thuộc AB, F thuộc CD sao cho (AE = CF); lấy các điểm G thuộc BC, H thuộc AD sao cho (BG = DH.)
Giải bài 3.19 trang 37 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
Cho tam giác ABC không vuông tại A. Dựng bên ngoài tam giác đó hai tam giác ABD, ACE vuông cân tại đỉnh A rồi dựng hình bình hành AEID.
Giải bài 3.12 trang 37 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
Xét hai hình bình hành MNBA và MNCB. a) Chứng minh A, B, C là ba điểm thẳng hàng;