Bài 2. Vận dụng đạo hàm giải bài toán tối ưu - Chuyên đ..

Giải bài 3 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

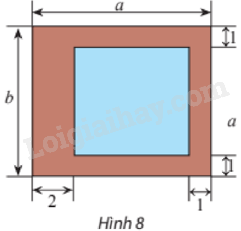
Người ta muốn thiết kế một lồng nuôi cá có bề mặt hình chữ nhật bao gồm phần mặt nước có diện tích bằng 54 m2 và phần đường đi xung quanh với kích thước (đơn vị: m) như Hình 8. Bề mặt của lồng có chiều dài và chiều rộng bằng bao nhiêu để diện tích phần đường đi là bé nhất?

Đề bài

Người ta muốn thiết kế một lồng nuôi cá có bề mặt hình chữ nhật bao gồm phần mặt nước có diện tích bằng 54 m² và phần đường đi xung quanh với kích thước (đơn vị: m) như Hình 8. Bề mặt của lồng có chiều dài và chiều rộng bằng bao nhiêu để diện tích phần đường đi là bé nhất?

Phương pháp giải - Xem chi tiết

• Tìm mối quan hệ giữa \(a,b\), biểu thị diện tích phần đường đường đi thông qua các đại lượng đã biết và ẩn.

• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm:

‒ Lập bảng biến thiên của hàm số trên tập hợp đó.

‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.

Lời giải chi tiết

Diện tích phần mặt nước là: \(\left( {a - 2 - 1} \right)\left( {b - 1 - 1} \right) = \left( {a - 3} \right)\left( {b - 2} \right)\) với \(a > 3,b > 2\).

Do phần mặt nước có diện tích bằng 54 m² nên ta có:

\(\left( {a - 3} \right)\left( {b - 2} \right) = 54 \Leftrightarrow b - 2 = \frac{{54}}{{a - 3}} \Leftrightarrow b = \frac{{54}}{{a - 3}} + 2\)

Diện tích bể là: \(ab = a.\left( {\frac{{54}}{{a - 3}} + 2} \right) = \frac{{54a}}{{a - 3}} + 2a\).

Diện tích phần đường đi xung quanh là: \(S = \frac{{54a}}{{a - 3}} + 2a - 54 = \frac{{162}}{{a - 3}} + 2a\).

Xét hàm số \(S\left( a \right) = \frac{{162}}{{a - 3}} + 2a\) trên khoảng \(\left( {3; + \infty } \right)\).

Ta có: \(S'\left( a \right) = - \frac{{162}}{{{{\left( {a - 3} \right)}^2}}} + 2\)

\(S'\left( a \right) = 0 \Leftrightarrow - \frac{{162}}{{{{\left( {a - 3} \right)}^2}}} + 2 = 0 \Leftrightarrow {\left( {a - 3} \right)^2} = 81 \Leftrightarrow a = 12\) hoặc \({\rm{a}} = - 6\) (loại).

Bảng biến thiên của hàm số trên khoảng \(\left( {3; + \infty } \right)\):

Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{\left( {3; + \infty } \right)} f\left( x \right) = f\left( {12} \right) = 42\).

Vậy diện tích phần đường đi \(S\) đạt giá trị nhỏ nhất khi \(a = 12\left( m \right)\) và \(b = \frac{{54}}{{12 - 3}} + 2 = 8\left( m \right)\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 4 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Một giếng dầu ngoài khơi được đặt ở vị trí \(A\) cách bờ biển 3 km, \(B\) là vị trí trên bờ biển gần giếng dầu nhất. Nhà máy lọc dầu được đặt ở vị trí \(C\) trên bờ biển, cách vị trí \(B\) một khoảng 4 km (Hình 9). Người ta dự định lắp đặt đường ống dẫn dầu gồm hai đoạn thẳng \(AD\) và \(DC\) (\(D\) là một vị trí nằm giữa \(B\) và \(C\)). Biết rằng mỗi mét đường ống đặt dưới biển có chi phí lắp đặt cao gấp đôi so với mỗi mét đường ống đặt trên bờ. Vị trí của \(D\) như thế nào để giảm thiểu chi p
Giải bài 5 trang 21 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Tại một xí nghiệp, nếu trong một tuần xí nghiệp sản xuất \(x\) nghìn sản phẩm thì chi phí sản xuất gồm: 10 triệu đồng chi phí cố định, 3 triệu đồng cho mỗi nghìn sản phẩm và \(0,001{x^2}\) triệu đồng chi phí bảo dưỡng thiết bị. a) Tính chi phí trung bình trên mỗi nghìn sản phẩm theo \(x\). b) Mỗi tuần xí nghiệp cần sản xuất bao nhiêu sản phẩm để chi phí trung bình thấp nhất?
Giải bài 2 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Người ta muốn xây một bể bơi có dạng hình hộp chữ nhật, thể tích 1800 m3 và chiều sâu 2 m (Hình 7). Biết rằng chi phí xây mỗi đơn vị diện tích của đáy bể gấp hai lần so với thành bể. Cần chọn chiều dài và chiều rộng của bể bằng bao nhiêu để tiết kiệm chi phí xây dựng bể nhất?
Giải bài 1 trang 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Người ta muốn xây một đường cống thoát nước có mặt cắt ngang là hình tạo bởi một nửa hình tròn ghép với một hình chữ nhật (Hình 6). Biết rằng mặt cắt ngang có diện tích 2 m2. Các kích thước \(x,y\) (đơn vị: m) bằng bao nhiêu để chu vi của mặt cắt ngang là nhỏ nhất? Tính chu vi nhỏ nhất đó.
Giải mục 2 trang 18, 19, 20 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Tại một xưởng sản xuất, chi phí để sản xuất (x) sản phẩm mỗi tháng là (Cleft( x right) = 5000 + 50x + 0,005{x^2}) (nghìn đồng). a) Tính chi phí trung bình để sản xuất một sản phẩm. b) Mỗi tháng xưởng sản xuất bao nhiêu sản phẩm thì chi phí trung bình để sản xuất một sản phẩm thấp nhất?
Giải mục 1 trang 15, 16, 17, 18 Chuyên đề học tập Toán 12 - Chân trời sáng tạo
Người ta muốn sản xuất những chiếc thùng có dạng hình hộp chữ nhật không nắp, có đáy là hình vuông và thể tích chứa là (500d{m^3}) (Hình 1). Biết rằng chiều cao của thùng trong khoảng từ (3dm) đến (10dm). a) Nếu gọi độ dài cạnh đáy của thùng là (xleft( {dm} right)), chiều cao của thùng là (hleft( {dm} right)) thì tổng diện tích các mặt của thùng, kí hiệu (S), có thể được biểu thị bằng biểu thức nào? b) Có thể biểu thị tổng diện tích (S) theo (x) không? Biến (x) nhận giá t