Đề thi học kì 2 môn toán lớp 7 năm 2019 - 2020 trường THCS Dịch Vọng

Đề bài

PHẦN TRẮC NGHIỆM (2 điểm) Chọn phương án đúng.

Câu 1 : Đơn thức nào sau đây đồng dạng với đơn thức $- 3x{y^2}?$

A. $- 3{x^2}y$               B. $\left( { - 3xy} \right)y$          

C.  $- 3{\left( {xy} \right)^2}$             D. $- 3xy$

Câu 2 : Giá trị $x = 2$ là nghiệm của đa thức nào sau đây ?

A. $f\left( x \right) = 2 + x$               B. $f\left( x \right) = {x^2} - 2$          

C.  $f\left( x \right) = x - 2$             D. $f\left( x \right) = x\left( {x + 2} \right)$

Câu 3 : Nếu $AM$ là đường trung tuyến và $G$ là trọng tâm của tam giác $ABC$ thì :

A. $GM = \dfrac{1}{3}AG$               B. $AM = \dfrac{2}{3}AG$          

C.  $AG = \dfrac{1}{3}AM$             D. $GM = \dfrac{1}{3}AM$

Câu 4 : Bộ ba đoạn thẳng nào sau đây có thể là độ dài ba cạnh của một tam giác :

A. $2cm;3cm;5cm$               B. $7cm;9cm;10cm$          

C.  $2cm;7cm;11cm$             D. $3cm;3cm;7cm$

PHẦN TỰ LUẬN (8 điểm)

Bài 1 (1,0 điểm) : Cho đa thức $f\left( x \right) =  - 2{x^3} + x - 1 + 4{x^2} - 5x + 3{x^3}$

a) Thu gọn và sắp xếp đa thức $f\left( x \right)$ theo lũy thừa giảm dần của biến

b) Tìm hệ số tự do và bậc của đa thức $f\left( x \right).$

Bài 2 (1,5 điểm) : Cho hai đa thức $A\left( x \right) = 2{x^2} - 5x + 3$ và $B\left( x \right) = {x^2} + 4x - 2$

a) Tính $A\left( x \right) + B\left( x \right)$

b) Tính $A\left( x \right) - B\left( x \right)$

c) Chứng tỏ $x = 1$ là nghiệm của đa thức $A\left( x \right).$

Bài 3 (1,5 điểm) : Tìm nghiệm của mỗi đa thức sau :

a) $3x - \dfrac{2}{5}$

b) $\left( {x - 3} \right)\left( {2x + 8} \right)$

Bài 4 (3,5 điểm) : Cho tam giác $ABC$ cân tại $A,$ vẽ trung tuyến $AM.$ Từ $M$ kẻ $ME$ vuông góc với $AB$ tại $E,$ kẻ $MF$ vuông góc với $AC$ tại $F$

a) Chứng minh $\Delta BEM = \Delta CFM$

b) Chứng minh $AM$ là đường trung trực của đoạn thẳng $EF$

c) Chứng minh $EF//BC$

d) Từ B kẻ đường thẳng vuông góc với AB tại B, từ C kẻ đường thẳng vuông góc với AC tại C, hai đường thẳng này cắt nhau ở D. Chứng minh ba điểm A, M, D thẳng hàng.

Bài 5 (0,5 điểm) : Cho $f\left( x \right) = a{x^2} + bx + c$ với $a,b,c$ là các số hữu tỉ.

Biết $13a + b + 2c = 0,$ chứng tỏ rằng : $f\left( { - 2} \right).f\left( 3 \right) \le 0$.

HẾT

Đ/a TN

 Câu 1 :

Phương pháp : 

Sử dụng :  Hai đơn thức đồng dạng với nhau nếu chúng phần hệ số khác $0$ và có cùng phần biến

Cách giải:

Ta có $\left( { - 3xy} \right)y =  - 3xy.y$ $=  - 3x{y^2}$ nên đơn thức $- 3x{y^2}$ đồng dạng với đơn thức $\left( { - 3xy} \right)y$

Chọn B

Câu 2 :

Phương pháp :

Sử dụng :  Số ${x_0}$ là nghiệm của đa thức $f\left( x \right)$ nếu $f\left( {{x_0}} \right) = 0$

Cách giải:

Thay ${x_0} = 2$ vào $f\left( x \right) = 2 + x$ ta được $f\left( 2 \right) = 2 + 2$$= 4 \ne 0$

Thay ${x_0} = 2$ vào $f\left( x \right) = {x^2} - 2$ ta được $f\left( 2 \right) = {2^2} - 2$$= 2 \ne 0$

Thay ${x_0} = 2$ vào $f\left( x \right) = x - 2$ ta được $f\left( 2 \right) = 2 - 2$$= 0$

Thay ${x_0} = 2$ vào $f\left( x \right) = x\left( {x + 2} \right)$ ta được $f\left( 2 \right) = 2\left( {2 + 2} \right)$$= 8 \ne 0$

Vậy $x = 2$ là nghiệm của đa thức $f\left( x \right) = x - 2$

Chọn C

Câu 3 :

Phương pháp :

Sử dụng :  Trong tam giác, trọng tâm cách đỉnh một khoảng bằng $\dfrac{2}{3}$ độ dài đường trung tuyến ứng với đỉnh đó.

Cách giải:

Vì $AM$ là đường trung tuyến và $G$ là trọng tâm của tam giác $ABC$ nên $AG = \dfrac{2}{3}AM$

Suy ra $GM = \dfrac{1}{3}AM$.

Chọn A

Câu 4:

Phương pháp :

Sử dụng bất đẳng thức tam giác : Tam giác có ba cạnh có độ dài $a,b,c$ thì $b - c < a < b + c$

Cách giải:

Ta thấy bộ ba số $7cm;9cm;10cm$ có $9 - 7 < 10 < 9 + 7$ $\left( {2 < 10 < 16} \right)$ thỏa mãn bất đẳng thức tam giác nên bộ ba số $7cm;9cm;10cm$ là độ dài ba cạnh của một tam giác.

Đáp án A sai vì $2 + 3 = 5$

Đáp án C sai vì $2 + 7 < 11$

Đáp án D sai vì $3 + 3 < 7$

Chọn B

LG bài 1

Phương pháp giải:

a) Thu gọn các đơn thức đồng dạng rồi sắp xếp theo lũy thừa giảm dần của biến

b) Hệ số tự do là hệ số của lũy thừa bậc 0 của biến

Bậc của đa thức một biến (khác 0, đã thu gọn) là số mũ lớn nhất của biến trong đa thức đó

Lời giải chi tiết:

a) $f\left( x \right) =  - 2{x^3} + x - 1 + 4{x^2} - 5x + 3{x^3}$

$= \left( { - 2{x^3} + 3{x^3}} \right) + \left( {x - 5x} \right)$ $- 1 + 4{x^2}$

$= {x^3} - 4x - 1 + 4{x^2}$ 

Ta sắp xếp như sau : $f\left( x \right) = {x^3} + 4{x^2} - 4x - 1$

b) Hệ số tự do là : $- 1$

Bậc của đa thức là : $3$

LG bài 2

Phương pháp giải:

a) b) Đặt phép tính theo hàng ngang (hoặc hàng dọc) rồi cộng trừ các đơn thức đồng dạng (nếu có)

c) Số $x = {x_0}$ là nghiệm của đa thức $f\left( x \right)$ nếu $f\left( {{x_0}} \right) = 0$

Lời giải chi tiết:

a) $A\left( x \right) + B\left( x \right)$

$= 2{x^2} - 5x + 3$$+ \left( {{x^2} + 4x - 2} \right)$

$= 2{x^2} - 5x + 3$$+ {x^2} + 4x - 2$

$= \left( {2{x^2} + {x^2}} \right) + \left( { - 5x + 4x} \right)$ $+ \left( {3 - 2} \right)$

$= 3{x^2} - x + 1$

Vậy $A\left( x \right) + B\left( x \right)$$= 3{x^2} - x + 1$

b) $A\left( x \right) - B\left( x \right)$

$= 2{x^2} - 5x + 3$$- \left( {{x^2} + 4x - 2} \right)$

$= 2{x^2} - 5x + 3$$- {x^2} - 4x + 2$

$= \left( {2{x^2} - {x^2}} \right) + \left( { - 5x - 4x} \right)$ $+ \left( {3 + 2} \right)$

$= {x^2} - 9x + 5$

Vậy $A\left( x \right) - B\left( x \right)$$= {x^2} - 9x + 5$

c) Thay $x = 1$ vào đa thức $A\left( x \right)$ ta được :

$A\left( 1 \right) = {2.1^2} - 5.1 + 3$ $= 2 - 5 + 3$ $=  - 3 + 3 = 0$

Vậy $x = 1$ là nghiệm của đa thức $A\left( x \right).$

LG bài 3

Phương pháp giải:

Sử dụng :  Để tìm nghiệm của đa thức $f\left( x \right)$, ta tìm $x = {x_0}$ thỏa mãn $f\left( {{x_0}} \right) = 0$

Lời giải chi tiết:

a) Xét $3x - \dfrac{2}{5} = 0$

$\begin{array}{l}3x = \dfrac{2}{5}\\x = \dfrac{2}{5}:3\\x = \dfrac{2}{5}.\dfrac{1}{3}\\x = \dfrac{2}{{15}}\end{array}$

Vậy $x = \dfrac{2}{{15}}$ là nghiệm của đa thức $3x - \dfrac{2}{5}$

b) Xét $\left( {x - 3} \right)\left( {2x + 8} \right) = 0$

TH1 : $x - 3 = 0$

$x = 3$

TH2 : $2x + 8 = 0$

$\begin{array}{l}2x =  - 8\\x =  - 8:2\\x =  - 4\end{array}$

Vậy $x = 3;x =  - 4$ là nghiệm của đa thức $\left( {x - 3} \right)\left( {2x + 8} \right)$

LG bài 4

Phương pháp giải:

a) Chứng minh hai tam giác vuông bằng nhau theo trường hợp cạnh huyền – góc nhọn.

b) Gọi H là giao điểm của AM và EF.

Chứng minh AH vuông góc với EF và $AH \bot EF$ bằng cách xét hai tam giác $\Delta AEH$ và $\Delta AFH$ 

c) Sử dụng định lý từ vuông góc đến song song: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song.

d) Chứng minh $\Delta ABD = \Delta ACD\left( {ch - cgv} \right)$ suy ra D nằm trên đường phân giác của góc A.

Lời giải chi tiết:

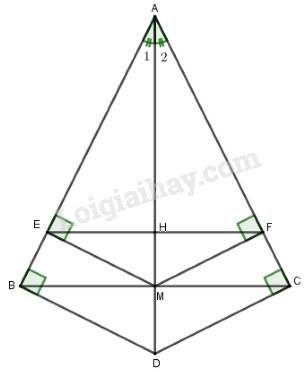
a) AM là trung tuyến của tam giác ABC nên MB = MC

Tam giác ABC cân tại A nên $\widehat B = \widehat C$.

$ME \bot AB$ tại E nên $\widehat {BEM} = {90^0}$

$MF \bot AB$ tại F nên $\widehat {CFM} = {90^0}$

Xét tam giác BEM và tam giác CFM có:

$\begin{array}{l}\widehat {BEM} = \widehat {CFM}\left( { = {{90}^0}} \right)\\BM = CM\left( {cmt} \right)\\\widehat B = \widehat C\left( {cmt} \right)\\ \Rightarrow \Delta BEM = \Delta CFM\left( {ch - gn} \right)\end{array}$

b)

Gọi $H$ là giao điểm của $AM$ với $EF$. 

Tam giác ABC cân tại A nên AM là đường trung tuyến của tam giác nên cũng là đường phân giác

$\Rightarrow \widehat {{A_1}} = \widehat {{A_2}}$

Theo câu a, $\Delta BEM = \Delta CFM \Rightarrow BE = CM$ (cạnh tương ứng)

$\begin{array}{l}AB = AC;BE = CF\\ \Rightarrow AB - BE = AC - CF\\ \Rightarrow AE = AF\end{array}$

Xét $\Delta AEH$ và $\Delta AFH$ có:

$\begin{array}{l}AE = AF\left( {cmt} \right)\\\widehat {{A_1}} = \widehat {{A_2}}\left( {cmt} \right)\\AH\,\,\,chung\\ \Rightarrow \Delta AEH = \Delta AFH\left( {c - g - c} \right)\end{array}$

$\Rightarrow HE = HF$ (cạnh tương ứng)  (1)

$\widehat {AHE} = \widehat {AHF}$ (góc tương ứng)

Mà

$\begin{array}{l}\widehat {AHE} + \widehat {AHF} = {180^0}\\ \Rightarrow \widehat {AHE} + \widehat {AHE} = {180^0}\\ \Rightarrow 2\widehat {AHE} = {180^0}\\ \Rightarrow \widehat {AHE} = {90^0}\\ \Rightarrow AH \bot EF\,\,\,\,\left( 2 \right)\end{array}$

Từ (1) và (2) suy ra $AM$ là đường trung trực của EF. (đpcm)

c)

Từ câu b) ta có $AM \bot EF$.

Tam giác ABC cân tại A nên AM là đường trung tuyến cũng là đường cao hay $AM \bot BC$

Vậy $EF//BC$ (từ vuông góc đến song song)

d)

$BD \bot AB \Rightarrow \widehat {ABD} = {90^0}$

$AC \bot CD \Rightarrow \widehat {ACD} = {90^0}$

Xét $\Delta ABD$ và $\Delta ACD$ có:

$\widehat {ABD} = \widehat {ACD} = {90^0}$

$AB = AC\left( {gt} \right)$

$AD$ chung

$\Rightarrow \Delta ABD = \Delta ACD\left( {ch - cgv} \right)$

$\Rightarrow \widehat {BAD} = \widehat {CAD}$ (góc tương ứng)

$\Rightarrow D$ nằm trên đường phân giác của góc $A$.

Mà $M$ cũng nằm trên đường phân giác của góc $A$.

Vậy ba điểm $A,D,M$ thẳng hàng (đpcm). 

LG bài 5

Phương pháp giải:

- Tính $f\left( { - 2} \right)$ và $f\left( 3 \right)$.

- Tính $f\left( { - 2} \right) + f\left( 3 \right)$ và nhận xét hai giá trị $f\left( { - 2} \right)$ và $f\left( 3 \right)$.

- Từ đó suy ra tích hai giá trị này.

Lời giải chi tiết:

$f\left( x \right) = a{x^2} + bx + c$

Ta có:

$\begin{array}{l}f\left( { - 2} \right) = a.{\left( { - 2} \right)^2} + b.\left( { - 2} \right) + c\\ = 4a - 2b + c\\f\left( 3 \right) = a{.3^2} + b.3 + c\\ = 9a + 3b + c\\ \Rightarrow f\left( { - 2} \right) + f\left( 3 \right)\\ = \left( {4a - 2b + c} \right) + \left( {9a + 3b + c} \right)\\ = 4a - 2b + c + 9a + 3b + c\\ = 13a + b + 2c = 0\\ \Rightarrow f\left( { - 2} \right) + f\left( 3 \right) = 0\\ \Rightarrow f\left( { - 2} \right) = 0 - f\left( 3 \right)\\ \Rightarrow f\left( { - 2} \right) =  - f\left( 3 \right)\\ \Rightarrow f\left( { - 2} \right).f\left( 3 \right) = \left[ { - f\left( 3 \right)} \right].f\left( 3 \right)\\ =  - {\left[ {f\left( 3 \right)} \right]^2}\end{array}$

Vì ${\left[ {f\left( 3 \right)} \right]^2} \ge 0$ nên $- {\left[ {f\left( 3 \right)} \right]^2} \le 0$

Vậy $f\left( { - 2} \right).f\left( 3 \right) \le 0$ (đpcm). 

HẾT

Loigiaihay.com