20 bài tập Công của lực điện mức độ vận dụng
Làm đề thiCâu hỏi 1 :
Cho điện tích q dịch chuyển giữa hai điểm cố định trong một điện trường đều với cường độ 150V/m thì công của lực điện trường là 60mJ. Nếu cường độ điện trường là 200V/m thì công của lực điện trường dịch chuyển điện tích q giữa hai điểm đó là:
- A 40J.
- B 40mJ.
- C 80J.
- D 80mJ
Đáp án: D
Phương pháp giải:
Công của lực điện : A = qEd
Lời giải chi tiết:
Công thức : A = q.E.d => A tỉ lệ thuận với E \( \Rightarrow {{{A_1}} \over {{A_2}}} = {{{E_1}} \over {{E_2}}} \Leftrightarrow {{{{60.10}^{ - 3}}} \over {{A_2}}} = {{150} \over {200}} \Rightarrow {A_2} = {80.10^{ - 3}}J = 80.mJ\)
Câu hỏi 2 :
Một electron chuyển động dọc theo đường sức của một điện trường đều. Cường độ điện trường có độ lớn là \(100\,\,V/m\). Vận tốc ban đầu của electron là \({3.10^5}\,\,m/s\), khối lượng là \(m = 9,{1.10^{ - 31}}\,\,kg\). Từ lúc bắt đầu chuyển động đến khi vận tốc bằng \(0\) thì electron đi được quãng đường là
- A \(5,12\,\,m\)
- B \(5,12\,\,mm\)
- C \(0,256\,\,m\)
- D \(2,56\,\,mm\)
Đáp án: D
Phương pháp giải:
Áp dụng định luật bảo toàn và chuyển hóa năng lượng: Độ giảm động năng của electron chính là công của lực điện tác dụng lên electron:
\(A = qE.d = {W_{ds}} - {W_{dtr}}\)
Lời giải chi tiết:
Áp dụng công thức về định luật bảo toàn và chuyển hóa năng lượng: Độ giảm động năng của electron chính là công của lực điện tác dụng lên electron:
\(\begin{array}{l}
A = qE.d = {{\rm{W}}_{ds}} - {{\rm{W}}_{dt}} \Rightarrow d = \frac{{\Delta {{\rm{W}}_d}}}{{q.E}} = \frac{{\frac{1}{2}.{m_e}.v_0^2}}{{q.E}}\\
\Rightarrow d = \frac{1}{2}.\frac{{9,{{1.10}^{ - 31}}.{{\left( {{{3.10}^5}} \right)}^2}}}{{1,{{6.10}^{ - 19}}.100}} = 25,{59.10^{ - 4}}\,\,\left( m \right) = 2,559\,\,\left( {mm} \right)
\end{array}\)
Chọn D.
Câu hỏi 3 :
Khi điện tích dịch chuyển trong điên trường đều theo chiều đường sức thì nó nhận được công là 10J; Khi dịch chuyển tạo với chiều đường sức 600 trên cùng độ dài quãng đường thì nó nhận được một công là:
- A 7,5J.
- B
\(\frac{{5\sqrt 3 }}{2}J\) - C 5J.
- D \(5\sqrt 2 J\)
Đáp án: C
Phương pháp giải:
vận dụng công thức A = qEd.cosα
Lời giải chi tiết:
Ta có A = qEd
.=> A’ = qEd.cosα = A.cos α = 10.cos 600 = 5J
Câu hỏi 4 :
Một electron bay dọc theo hướng đường sức của điện trường đều với vận tốc tại A là 5.106, sau đó dừng lại tại B với AB = d = 10cm (A, B đều nằm trong điện trường). Độ lớn của cường độ điện trường E?
- A 7109,4V/m
- B 355,47V/m
- C 170,9 V/m
- D 710,94 V/m
Đáp án: D
Phương pháp giải:
Phương pháp: Áp dụng định lí động năng
Lời giải chi tiết:
Hướng dẫn giải:
Ta có, khi electron di chuyển từ A đến B thì chịu tác dụng của ngoại lực là lực điện trường nên theo định lí động năng, ta có:
\({{\rm{W}}_{{d_B}}} - {{\rm{W}}_{{d_A}}} = {A_{ngoailuc}} \leftrightarrow 0 - \frac{1}{2}mv_A^2 = qE{{\rm{d}}_{AB}} \to E = \frac{{mv_A^2}}{{2\left| {q{{\rm{d}}_{AB}}} \right|}} = \frac{{9,{{1.10}^{ - 31}}.{{({{5.10}^6})}^2}}}{{2\left| {{\rm{ - 1,6}}{\rm{.1}}{{\rm{0}}^{ - 19}}{\rm{.0,1}}} \right|}} = 710,94V/m\)
=> Chọn D
Câu hỏi 5 :
Hai tấm kim loại đặt song song, cách nhau 2cm, được nhiễm điện trái dấu nhau và có độ lớn bằng nhau. Muốn điện tích q = 5.10-10 C di chuyển từ tấm này đến tấm kia cần tốn một công A = 2.10-9 J. Hãy xác định cường độ điện trường bên trong hai tấm kim loại đó. Cho biết điện trường bên trong hai tấm kim loại đã cho là điện trường đều và có đường sức vuông góc với các tấm.
- A 100V/m
- B 150V/m
- C 200V/m
- D 300V/m
Đáp án: C
Phương pháp giải:
Phương pháp:
Công của lực điện: A = qEd
Lời giải chi tiết:
Cách giải:
Công của lực điện trường tác dụng lên điện tích q khi di chuyển trong điện trường đều E là: A = q.E.d
→ Cường độ điện trường bên trong hai tấm kim loại:
\(E = \frac{A}{{q.d}} = \frac{{{{2.10}^{ - 9}}}}{{{{5.10}^{ - 10}}{{.2.10}^{ - 2}}}} = 200\left( {V/m} \right)\)
Chọn C
Câu hỏi 6 :
Lực điện trường sinh công \(9,{6.10^{ - 18}}J\) dịch chuyển electron
\(\left( {e{\rm{ }} = {\rm{ }} - 1,{{6.10}^{ - 19}}C,{\rm{ }}{m_e} = {\rm{ }}9,{{1.10}^{ - 31}}kg} \right)\) dọc theo đường sức điện trường đi được quãng đường \(0,6cm\). Nếu đi thêm một đoạn \(0,4cm\) nữa theo chiều như cũ thì vận tốc của electron ở cuối đoạn đường là? Giả sử ban đầu electron đang ở trạng thái đứng yên.
- A \(2,{11.10^{13}}m/s\)
- B \({75.10^5}m/s\)
- C \({45.10^5}m/s\)
- D \(2,{75.10^{13}}m/s\)
Đáp án: B
Phương pháp giải:
Phương pháp:
+ Áp dụng biểu thức tính công của lực điện trường: \(A{\rm{ }} = {\rm{ }}qEd\)
+ Vận dụng biểu thức: \({A_{MN\;}} = {\rm{ }}{W_{{d_N}}} - {\rm{ }}{W_{{d_M}}}\)
Lời giải chi tiết:
Hướng dẫn giải:
Gọi \({A_1}\) - là công của lực điện trường khi dịch chuyển electron quãng đường \(0,6cm\)
\({A_2}\) - là công của lực điện trường khi dịch chuyển electron quãng đường \({s_2} = 0,6 + 0,4 = 1cm\)
Ta có:
\(\begin{array}{*{20}{l}}{{A_1} = {\rm{ }}9,{{6.10}^{ - 18}}J,{\rm{ }}{s_1} = {\rm{ }}0,6cm,{\rm{ }}e{\rm{ }} = {\rm{ }} - 1,{{6.10}^{ - 19}}C,{\rm{ }}{m_e} = {\rm{ }}9,{{1.10}^{ - 31}}kg}\\{{s_2} = {\rm{ }}0,4{\rm{ }} + {\rm{ }}0,6{\rm{ }} = {\rm{ }}1cm,{\rm{ }}{v_0} = {\rm{ }}0}\end{array}\)
Lực điện sinh công dương => electron chuyển động ngược chiều điện trường \(\alpha = {\rm{ }}{180^0}\)
\({A_1} = qE{s_1}cos\alpha \to E = \frac{{{A_1}}}{{e.{s_1}{\rm{cos18}}{{\rm{0}}^0}}} = \frac{{9,{{6.10}^{ - 18}}}}{{ - 1,{{6.10}^{ - 19}}.0,006.{\rm{cos18}}{{\rm{0}}^0}}} = {10^4}V/m\)
Mặt khác, ta có: \({A_{1\;}}{\rm{ = }}{W_{{d_1}}} - {W_{{d_0}}} = {1 \over 2}m{v_1}^2 - {1 \over 2}m{v_0}^2 = {1 \over 2}m{v_1}^2\)
\(\begin{array}{l}{A_2} = qE{s_2}cos\alpha = 1,{6.10^{ - 17}}J\\{A_{2\;}}{\rm{ = }}{W_{{d_2}}} - {W_{{d_1}}} = \frac{1}{2}m{v_2}^2 - \frac{1}{2}m{v_1}^2 = \frac{1}{2}m{v_2}^2 - {A_1}\\ \to \frac{1}{2}m{v_2}^2 = {A_{2\;}} + {A_{1\;}} \to {v_2} = \sqrt {\frac{{2({A_{2\;}} + {A_{1\;}})}}{m}} = \sqrt {\frac{{2(9,{{6.10}^{ - 18}} + 1,{{6.10}^{ - 17}})}}{{9,{{1.10}^{ - 31}}}}} = {75.10^5}m/s\end{array}\)
=> Chọn B
Câu hỏi 7 :
Một electron được thả không vận tốc ban đầu ở sát bản âm, trong điện trường đều giữa hai bản kim loại phẳng, tích điện trái dấu. Cường độ điện trường giữa hai bản là 1000V/m. Khoảng cách giữa hai bản là 1 cm. Tính động năng của electron khi nó đến đập vào bản dương.
- A - 1,6.10-16 J
- B + 1,6.10-16 J
- C - 1,6.10-18 J
- D + 1,6.10-18 J
Đáp án: D
Phương pháp giải:
Phương pháp:
- Định lí động năng: Độ biến thiên động năng của một vật bằng công của ngoại lực tác dụng lên vật.
- Công của lực điện: A = qEd
Lời giải chi tiết:
Cách giải:
Electron bị bản âm đẩy và bản dương hút nên di chuyển từ bản âm về bản dương và lực điện sinh công dương.
Điện trường giữa hai bản là điện trường đều E = 1000 V/m.
Áp dụng định lí động năng ta có:
\({W_d}\;-{\rm{ }}0 = qEd = - 1,{6.10^{ - 19}}.1000.\left( { - {{1.10}^{ - 2}}} \right)\; = {\rm{ }}1,{6.10^{ - 18}}J\)
Động năng của electron khi nó đập đến bản dương là Wđ = 1,6.10-18J.
Chọn D
Câu hỏi 8 :
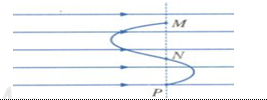
Một điện tích q chuyển động từ điểm M đến điểm N, từ điểm N đến điểm P như trên hình vẽ thì công của lực điện trong mỗi trường hợp bằng bao nhiêu ?
- A AMN = ANP = 0
- B AMN = 1,5ANP
- C AMN > 0; ANP < 0
- D AMN < 0; ANP > 0
Đáp án: A
Phương pháp giải:
Phương pháp:
- Công của lực điện: A = Fs.cosα = qEd = WM - WN
- Công của lực điện trong sự di chuyển của một điện tích không phụ thuộc hình dạng đường đi mà chỉ phụ thuộc vị trí điểm đầu và điểm cuối của đường đi trong điện trường.
Lời giải chi tiết:
Cách giải:
Cách 1:
Vì M, N, P nằm trên cùng một đường thẳng vuông góc với đường sức của điện trường đều nên hình chiếu của điểm đầu và điểm cuối đường đi trùng nhau tại một điểm (d = 0), nên công của lực điện trong hai trường hợp: AMN = ANP = 0
Cách 2:
Vì M, N, P nằm trên cùng một đường thẳng vuông góc với đường sức của điện trường đều, nên điện thế của các điểm này bằng nhau: VM = VN = VP
Mặt khác: AMN = WM - WN = q.(VM - VN)
ANP = WN - WP = q.(VN - VP)
→ AMN = ANP = 0
Chọn A
Câu hỏi 9 :
Có hai điện tích điểm q1 và q2 = 4q1 dịch chuyển trong điện trường đều theo các quỹ đạo tròn có bán kính tương ứng là R1 và R2 = 2R1. Công của lực điện thực hiện lên hai điện tích q1, q2 lần lượt là A1và A2. Biểu thức nào dưới đây là đúng?
- A \({A_1} = 8{A_2}\)
- B \({A_1} = 0,5{A_2}\)
- C \({A_1} = {A_2}\)
- D \({A_1} = 2{A_2}\)
Đáp án: C
Lời giải chi tiết:
Lực điện đóng vai trò là lực hướng tâm trong chuyển động tròn của các điện tích nên công của lực điện bằng 0.
Câu hỏi 10 :
Giả thiết rằng một tia sét có điện tích q = 25 C được phóng từ đám mây dông xuống mặt đất, khi đó hiệu điện thế giữa đám mây và mặt đất U = 1,4.108 V. Năng lượng của tia sét này làm bao nhiêu kilôgam nước ở 1000 C bốc thành hơi nước ở ? Biết nhiệt hóa hơi của nước bằng 2,3.106 J/kg.
- A 1521,7 kg.
- B 2247 kg.
- C 1120 kg.
- D 2172 kg.
Đáp án: A
Phương pháp giải:
áp dụng công thức tính công của lực điện tác dụng lên điện tích chuyển động trong từ trường
Lời giải chi tiết:
Đáp án A
+ Năng lượng của tia sét tương ứng với công của lực điện dịch chuyển các điện tích q trong hiệu điện thế U.
\( \to E = A = qU = {35.10^8}\,\,J.\)
+ Lượng nước hóa hơi tương ứng \(E = \lambda m \Rightarrow m = {E \over \lambda } = {{{{35.10}^8}} \over {2,{{3.10}^6}}} = 1521,7\,\,kg.\)
Câu hỏi 11 :
Cho điện tích q dịch chuyển giữa hai điểm cố định trong một điện trường đều với cường độ 150V/m thì công của lực điện trường là 60mJ. Nếu cường độ điện trường là 200V/m thì công của lực điện trường dịch chuyển điện tích q giữa hai điểm đó là:
- A 40J.
- B 40mJ.
- C 80J.
- D 80mJ
Đáp án: D
Phương pháp giải:
Công của lực điện : A = qEd
Lời giải chi tiết:
Công thức : A = q.E.d => A tỉ lệ thuận với E \( \Rightarrow {{{A_1}} \over {{A_2}}} = {{{E_1}} \over {{E_2}}} \Leftrightarrow {{{{60.10}^{ - 3}}} \over {{A_2}}} = {{150} \over {200}} \Rightarrow {A_2} = {80.10^{ - 3}}J = 80.mJ\)
Câu hỏi 12 :
Hiệu điện thế giữa hai điểm M, N trong điện trường là UMN = 100V. Gọi A1 là công điện trường làm dịch chuyển proton từ M đến N, A2 là công điện trường làm dịch chuyển electron từ M đến N. Chọn phương án nào sai?
- A A1 = A2
- B A1 < 0, A2 > 0
- C |A1| = |A2|
- D A1, A2> 0
Đáp án: C
Phương pháp giải:
Phương pháp: Áp dụng biểu thức tính công của điện trường: A = qU
Lời giải chi tiết:
Hướng dẫn giải:
Ta có:
+ Công điện trường thực hiện proton dịch chuyển từ M đến N.
\({A_1} = {q_p}.U_{MN}^{} = 1,{6.10^{ - 19}}.100 = 1,{6.10^{ - 17}}J\) J
+ Công điện trường thực hiện electron dịch chuyển từ M đến N.
\({A_2} = {q_e}.U_{MN}^{} = - 1,{6.10^{ - 19}}.100 = - 1,{6.10^{ - 17}}\,J\)
=> Chọn C
Câu hỏi 13 :
Một electron di chuyển một đoạn 0,6 cm từ điểm M đến điểm N dọc theo một đường sức điện của 1 điện trường đều thì lực điện sinh công 9,6.10-18J. Cường độ điện trường E bằng?
- A 104 V/m
- B 104 V/cm
- C 2.104 V/m
- D 16.103 V/m
Đáp án: A
Phương pháp giải:
Phương pháp: Áp dụng công thức xác định công của lực điện: A = qEd
Lời giải chi tiết:
Hướng dẫn giải:
Ta có: \({A_{MN}} = {\rm{ }}q.E.\overline {{M'}{N'}} \)
vì AMN > 0; q < 0; E > 0 nên \(\overline {{M'}{N'}} < 0\)tức là e đi ngược chiều đường sức. \( \to \overline {{M'}{N'}} = - 0,006{\rm{ }}\left( m \right)\)
Cường độ điện trường: \(E = \frac{{{A_{MN}}}}{{q.\overline {M'N'} }} = \frac{{9,{{6.10}^{ - 18}}}}{{\left( { - 1,{{6.10}^{ - 19}}} \right).\left( { - 0,006} \right)}} = {10^4}(V/m)\)
=> Chọn A
Câu hỏi 14 :
Một điện tích điểm di chuyển dọc theo đường sức của một điện trường đều có cường độ điện trường E = 1000 V/m, đi được một khoảng d = 5 cm.Lực điện trường thực hiện được công A = 15.10-5J. Độ lớn của điện tích đó là
- A 15.10-6C
- B 5.10-6C
- C 3.10-6C
- D 10-5C
Đáp án: C
Phương pháp giải:
Công của lực điện trường: A = |q|Ed
Lời giải chi tiết:
Công của lực điện trường: A = |q|Ed => 15.10-5 = |q|.1000.0,05 => |q| = 3.10-6C
Chọn C
Câu hỏi 15 :
Một electron di chuyển được đoạn đường 1 cm, dọc theo một đường sức điện, dưới tác dụng của lực điện trong một điện trường đều có cường độ điện trường 1000 V/m. Hỏi công của lực điện có giá trị nào sau đây ?
- A - 1,6.10-16 J
- B + 1,6.10-16 J
- C - 1,6.10-18 J
- D + 1,6.10-18 J
Đáp án: D
Phương pháp giải:
Phương pháp :
Công của lực điện: A = qEd = qEs.cosα
Lời giải chi tiết:
Cách giải :
Dưới tác dụng của lực điện, electron di chuyển ngược chiều điện trường (tức ngược chiều đường sức điện).
Ta có: \(\alpha = \left( {\overrightarrow F ,\overrightarrow d } \right) = {180^0} \Rightarrow A = {q_e}.E.s.\cos \alpha = - 1,{6.10^{ - 19}}{.1000.10^{ - 2}}.\cos 180 = 1,{6.10^{ - 18}}J\)
Chọn D
Câu hỏi 16 :
Cho điện tích dịch chuyển giữa 2 điểm cố định trong một điện trường đều với cường độ \(3000\,\,V/m\) thì công của lực điện trường là \(90\,\,mJ\). Nếu cường độ điện trường là \(4000\,\,V/m\) thì công của lực điện trường dịch chuyển điện tích giữa hai điểm đó là?
- A \(90\,\,mJ\)
- B \(120\,\,mJ\)
- C \(67,5\,\,mJ\)
- D \(150\,\,mJ\)
Đáp án: B
Phương pháp giải:
Công của lực điện: \(A = qEd\)
Trong đó, d là hình chiếu của quỹ đạo lên phương của đường sức điện.
Lời giải chi tiết:
Công của lực điện trường là:
\(\begin{array}{l}
\left\{ {\begin{array}{*{20}{l}}
{{A_{MN1}}\; = q{E_1}d}\\
{{A_{MN2}}\; = q{E_2}d}
\end{array}} \right. \Rightarrow \frac{{{A_{MN1}}}}{{{A_{MN2}}}} = \frac{{{E_1}}}{{{E_2}}}\\
\Rightarrow {A_{MN2}} = \frac{{{E_2}}}{{{E_1}}}.{A_{MN1}} = \frac{{4000}}{{3000}}.90 = 120\,\,\left( {mJ} \right)
\end{array}\)
Chọn B.
Câu hỏi 17 :
Một nguồn điện có suất điện động 200mV. Để chuyển một điện lượng 10C qua nguồn thì lực lạ phải sinh một công là:
- A 20J
- B 0,05J
- C 2000J
- D 2J
Đáp án: D
Lời giải chi tiết:
Câu hỏi 18 :
Một proton nằm cách electron khoảng r = 0,5.10-10m trong chân không. Vận tốc tối thiểu của proton để nó thoát khỏi sức hút của electron là?
- A 1,6.106 m/s
- B 10,24.106 m/s
- C 0,8.106 m/s
- D 3,2.106 m/s
Đáp án: D
Phương pháp giải:
Phương pháp:
+ Áp dụng biểu thức tính thế năng tương tác tĩnh điện: \({\rm{W}} = k\frac{{{e^2}}}{r}\)
+ Áp dụng biểu thức tính động năng: \({\rm{W}} = \frac{1}{2}m{v^2}\)
+ Áp dụng định luật bảo toàn năng lượng
Lời giải chi tiết:
Hướng dẫn giải:
Ta có:
+ Lúc đầu năng lượng của hệ là thế năng tương tác tĩnh điện: \({{\rm{W}}_1} = k\frac{{{e^2}}}{r}\)
+ Khi nó vừa thoát ra thì có vận tốc v, lúc này nó không chịu lực hút của electron nên lúc này hệ không còn thế năng tương tác mà chỉ có động năng: \({{\rm{W}}_2} = \frac{1}{2}m{v^2}\)
Áp dụng định luật bảo toàn năng lượng, ta có:
\({{\rm{W}}_1} = {{\rm{W}}_2} \leftrightarrow k\frac{{{e^2}}}{r} = \frac{1}{2}m{v_0}^2 \to {v_0} = \sqrt {\frac{{2{{\rm{e}}^2}}}{{m{\rm{r}}}}} = 3,{2.10^6}m/s\)
=> Chọn D
Câu hỏi 19 :
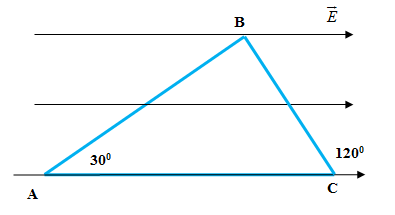
Một điện tích q = + 4.10-8C di chuyển trong một điện trường đều có cường độ E = 100 V/m theo một đường gấp khúc ABC. Đoạn AB dài 20 cm và vectơ độ dời \(\overrightarrow {AB} \) làm với các đường sức điện một góc 30o. Đoạn BC dài 40 cm và vectơ độ dời \(\overrightarrow {BC} \) làm với các đường sức điện một góc 120o. Tính công của lực điện khi điện tích di chuyển từ A đến C?
- A 1,5.10-6J
- B - 1,5.10-6J
- C 0,1.10-6J
- D – 0,1.10-6J
Đáp án: D
Phương pháp giải:
Phương pháp:
Công của lực điện: A = qEd = qEs.cosα
Lời giải chi tiết:
\(\begin{array}{*{20}{l}}{{A_{ABC}}\; = {A_{AB}}\; + {\rm{ }}{A_{BC}}}\\{{A_{AB}}\; = qE{d_1}\; = qE.AB.\cos 30 = {{4.10}^{ - 8}}.100.ABcos30\; = 0,{{7.10}^{ - 6}}J}\\{{A_{BC}}\; = qE{d_2} = qE.BC.\cos {{120}^o} = {{4.10}^{ - 8}}.100.BC.\cos 120\; = - 0,{{8.10}^{ - 6}}J}\\{ \Rightarrow {A_{ABC}}\; = {A_{AB}}\; + {\rm{ }}{A_{BC}} = - 0,{{1.10}^{ - 6}}J}\end{array}\)
Chọn D
Câu hỏi 20 :
Điện tích \(q = {10^{ - 8}}\,\,C\) di chuyển dọc theo các cạnh của tam giác đều ABC cạnh \(a = 10\,\,cm\) trong điện trường đều cường độ điện trường là \(E = 300\,\,V/m\), \(\overrightarrow E //BC\). Tính công của lực điện trường khi \(q\) di chuyển trên mỗi cạnh của tam giác:
- A \({A_{AB}}\; = 1,{5.10^{ - 7}}J;{A_{BC}} = - {3.10^{ - 7}}J;{A_{AC}} = 1,{5.10^{ - 7}}J\)
- B \({A_{AB}}\; = 1,{5.10^{ - 7}}J;{A_{BC}} = {3.10^{ - 7}}J;{A_{AC}} = - 1,{5.10^{ - 7}}J\)
- C \({A_{AB}}\; = - 1,{5.10^{ - 7}}J;{A_{BC}} = {3.10^{ - 7}}J;{A_{AC}} = 1,{5.10^{ - 7}}J\)
- D \({A_{AB}}\; = - 1,{5.10^{ - 7}}J;{A_{BC}} = {3.10^{ - 7}}J;{A_{AC}} = - 1,{5.10^{ - 7}}J\)
Đáp án: C
Phương pháp giải:
Công của lực điện: \(A = qEd\)
Trong đó, d là hình chiếu của quỹ đạo lên phương của đường sức điện.
Lời giải chi tiết:
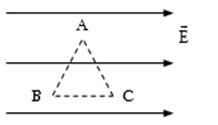
Công của lực điện trường khi q di chuyển trên cạnh AB là:
\({A_{AB}}\; = q.E.AB.cos{120^0} = {10^{ - 8}}.300.0,1.\left( { - 0,5} \right){\rm{ }} = - 1,{5.10^{ - 7}}\;J\)
Công của lực điện trường khi q di chuyển trên cạnh BC là:
\({A_{BC}}\; = q.E.BC = {10^{ - 8}}.300.0,1 = {3.10^{ - 7}}\;J\)
Công của lực điện trường khi q di chuyển trên cạnh AC là:
\({A_{AC}}\; = q.E.AC.cos60 = {10^{ - 8}}.300.0,1.0,5 = 1,{5.10^{ - 7}}\;J\)
Chọn C.
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- 40 bài tập Dòng điện trong chân không mức độ nhận biết, thông hiểu
- 40 bài tập Dòng điện trong chất khí mức độ nhận biết, thông hiểu
- 40 bài tập Dòng điện trong chất điện phân mức độ vận dụng
- 40 bài tập Dòng điện trong chất điện phân mức độ nhận biết, thông hiểu
- 40 bài tập dòng điện trong kim loại mức độ vận dụng
- 50 bài tập Định luật Ôm đối với toàn mạch mức độ vận dụng (Phần 2)
- 40 bài tập Dòng điện trong chân không mức độ nhận biết, thông hiểu
- 40 bài tập Dòng điện trong chất khí mức độ nhận biết, thông hiểu
- 40 bài tập Dòng điện trong chất điện phân mức độ vận dụng
- 40 bài tập Dòng điện trong chất điện phân mức độ nhận biết, thông hiểu