 Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
 Đề ôn tập học kì 2 – Có đáp án và lời giải
Đề ôn tập học kì 2 – Có đáp án và lời giải
Đề số 1 - Đề kiểm tra học kì 2 - Toán 7
Đáp án và lời giải chi tiết Đề số 1 - Đề kiểm tra học kì 2 - Toán 7
Đề bài
I. TRẮC NGHIỆM (2 ĐIỂM) Chọn chữ cái đứng trước câu trả lời đúng
Câu 1. Đơn thức đồng dạng với đơn thức \(\dfrac{1}{2}{x^4}{y^6}\) là:
A. \( - \dfrac{1}{2}{x^6}{y^4}\) B. \(\dfrac{1}{5}{x^4}{y^6}\)
C.\( - \dfrac{1}{2}{x^2}{y^8}\) D. \(\dfrac{4}{5}x{y^3}\)
Câu 2. Số điểm kiểm tra môn toán của mỗi bạn trong một tổ của lớp 8 được ghi lại như sau:
![]()
Số trung bình cộng là:
A. 8,7 B. 7,7 C. 8,6 D. 7,6
Câu 3. Nếu tam giác \(ABC\) có trung tuyến \(AM\) và \(G\) là trọng tâm thì
A. \(AG = GM\) B.\(GM = \dfrac{1}{2}AG\)
C. \(AG = \dfrac{1}{3}AM\) D. \(AM = 2.AG\)
Câu 4. Cho \(\Delta ABC\) có \(\angle A = {50^0}\,,\,\angle B = {90^0}\) thì quan hệ giữa ba cạnh \(AB,AC,BC\) là:
A. \(BC > AC > AB\)
B. \(AB > BC > AC\)
C. \(AB > AC > BC\)
D. \(AC > BC > AB\)
II. TỰ LUẬN (8 ĐIỂM)
Bài 1 (VD_1,0 điểm). Cho đơn thức \(A = \left( { - \dfrac{2}{3}x{y^2}} \right).\left( { - \dfrac{1}{4}{x^2}{y^3}} \right)\)
a) Thu gọn đơn thức \(A\).
b) Tính giá trị của đơn thức \(A\) khi \(x = 1;y = - 1\).
Bài 2 (VD_1,5 điểm): Cho các đa thức:
\(A\left( x \right) = 2\,{x^4} - 5\,{x^3} + 7\,x - 5\)\( + 4\,{x^3} + 3\,{x^2} + 2\,x + 3\)
\(B\left( x \right) = 5\,{x^4} - 3\,{x^3} + 5\,x - 3\,{x^4}\)\( - 2\,{x^3}\, + 9 - 6\,x\)
\(C\left( x \right) = {x^4} + 4\,{x^2} + 5\)
a) Thu gọn và sắp xếp các hạng tử của đa thức \(A\left( x \right),\,B\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Tính \(A\left( x \right) + B\left( x \right);\,A\left( x \right) - B\left( x \right)\).
c) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.
Bài 3 (VD_1,5 điểm): Tìm nghiệm của các đa thức sau:
\(a)\,2\,x + 5\) \(b)\,2\,{x^2} + \dfrac{2}{3}\)
\(c)\,\left( {x - 7} \right).\left( {{x^2} - \dfrac{9}{{16}}} \right)\)
Bài 4 (VD_3,5 điểm): Cho \(\Delta ABC\) vuông tại \(A\) có \(\angle C = {30^0},\) đường cao \(AH.\) Trên đoạn \(HC\) lấy điểm \(D\) sao cho \(HD = HB.\)
a) Chứng minh \(\Delta AHB = \Delta AHD\).
b) Chứng minh \(\Delta ABD\) là tam giác đều.
c) Từ \(C\) kẻ \(CE\) vuông góc với đường thẳng \(AD\)\(\left( {E \in \,AD} \right)\). Chứng minh \(DE = HB\).
d) Từ \(D\) kẻ \(DF\) vuông góc với \(AC\) (\(F\,\)thuộc \(AC\)), \(I\) là giao điểm của \(CE\) và \(AH.\) Chứng minh ba điểm \(I,\,D,\,F\) thẳng hàng.
Bài 5 (VDC_0,5 điểm): Chứng minh rằng đa thức \(P\left( x \right) = {x^3} - x + 5\) không có nghiệm nguyên.
Đ/a TN
Lời giải chi tiết:
|
1.B |
2.A |
3.B |
4.D |
Câu 1:
Phương pháp: Đơn thức đồng dạng là những đơn thức có cùng phần biến nhưng khác hệ số.
Cách giải: Đơn thức đồng dạng với đơn thức \(\dfrac{1}{2}{x^4}{y^6}\) là: \(\dfrac{1}{5}{x^4}{y^6}\).
Chọn B.
Câu 2:
Phương pháp: Muốn tìm trung bình cộng của n số ta tìm tổng của n số đó rồi chia cho n.
Cách giải:
Số trung bình cộng là:
\(\dfrac{{9 + 9 + 10 + 7 + 9 + 9 + 7 + 9 + 8 + 10}}{{10}} = 8,7\).
Chọn A.
Câu 3:
Phương pháp: Nếu \(\Delta ABC\) có trung tuyến \(AM\) và trọng tâm \(G\) thì \(AG = \dfrac{2}{3}AM\).
Cách giải:
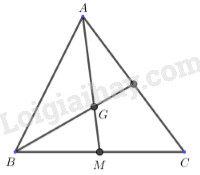
Nếu \(\Delta ABC\) có trung tuyến \(AM\) và trọng tâm \(G\) thì \(AG = \dfrac{2}{3}AM\).
Suy ra \(GM = \dfrac{1}{2}AG\).
Chọn B.
Câu 4:
Phương pháp: Dựa vào mối quan hệ giữa góc và cạnh trong tam giác để so sánh các cạnh với nhau.
Cách giải:
Ta có: \(\angle C = {180^0} - \left( {{{50}^0} + {{90}^0}} \right) = {40^0}\).
\( \Rightarrow \angle C < \angle A < \angle B\)
\( \Rightarrow AB < BC < AC\) hay \(AC > BC > AB\).
Chọn D.
LG bài 1
Phương pháp giải:
a) Để thu gọn đơn thức ta nhân phần hệ số với nhau, phần biến với nhau.
b) Thay \(x = 1;y = - 1\) vào đơn thức thu gọn của \(A\).
Lời giải chi tiết:
a) Thu gọn đơn thức:
\(\begin{array}{l}A = \left( { - \dfrac{2}{3}x{y^2}} \right).\left( { - \dfrac{1}{4}{x^2}{y^3}} \right)\\\,\,\,\,\, = - \dfrac{2}{3}.\left( {\dfrac{{ - 1}}{4}} \right).{x^3}.{y^5}\\\,\,\,\,\, = \,\dfrac{1}{6}.{x^3}.{y^5}\end{array}\)
b) Thay \(x = 1;y = - 1\) vào đơn thức \(A\) thu gọn ta được:
\(A = \dfrac{1}{6}{.1^3}.{\left( { - 1} \right)^5} = - \dfrac{1}{6}\).
Vậy giá tri của đơn thức \(A\) tại \(x = 1;y = - 1\) là \(A = - \dfrac{1}{6}.\)
LG bài 2
Phương pháp giải:
a) Thu gọn và sắp xếp các hạng tử của đa thức \(A\left( x \right),\,B\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Tính \(A\left( x \right) + B\left( x \right);\)\(\,A\left( x \right) - B\left( x \right)\).
c) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.
Lời giải chi tiết:
a) Thu gọn:
\(A\left( x \right) = 2\,{x^4} - 5\,{x^3} + 7\,x - 5\)\( + 4\,{x^3} + 3\,{x^2} + 2\,x + 3\)
\( = 2\,{x^4} + \left( { - 5\,{x^3} + 4\,{x^3}} \right) + 3{x^2}\)\( + \left( {7\,x + 2\,x} \right) - 5 + 3\)
\( = 2\,{x^4} - {x^3} + 3\,{x^2} + 9\,x\, - 2\)
\(B\left( x \right) = 5\,{x^4} - 3\,{x^3} + 5\,x - 3\,{x^4}\)\( - 2\,{x^3}\, + 9 - 6\,x\)
\( = \left( {5\,{x^4} - 3\,{x^4}} \right) + \left( { - 3\,{x^3} - 2\,{x^3}} \right)\)\( + \left( {5\,x - 6\,x} \right) + 9\)
\( = \,\,2\,{x^4}\, - \,5{x^3} - x + 9\)
b) Tính \(A\left( x \right) + B\left( x \right);\,A\left( x \right) - B\left( x \right)\).
\( + )\,A\left( x \right) + B\left( x \right) = \left( {2\,{x^4} - {x^3} + 3\,{x^2} + 9\,x - 2} \right)\)\( + \left( {2\,{x^4} - 5\,{x^3} - x + 9} \right)\)
\( = \left( {2\,{x^4} + 2\,{x^4}} \right) + \left( { - {x^3} - 5\,{x^3}} \right)\)\( + 3\,{x^2} + \left( {9\,x - x} \right) + \left( { - 2 + 9} \right)\)
\( = \,\,\,4\,{x^4} - 6\,{x^3} + 3\,{x^2} + 8\,x + 7\)
\( + )\,A\left( x \right) - B\left( x \right) = \left( {2\,{x^4} - {x^3} + 3\,{x^2} + 9\,x - 2} \right)\)\( - \left( {2\,{x^4} - 5\,{x^3} - x + 9} \right)\)
\( = \left( {2\,{x^4} - \,{x^3} + 3\,{x^2} + 9\,x - 2} \right)\)\( - 2\,{x^4} + 5\,{x^3} + x - 9\)
\( = \left( {2\,{x^4} - \,2\,{x^4}} \right) + \left( { - {x^3} + 5\,{x^3}} \right)\)\( + 3\,{x^2} + \left( {9\,x + x} \right) + \left( { - 2 - 9} \right)\)
\( = \,\,4\,{x^3} + \,3\,{x^2} + 10\,x - 11\)
c) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.
Ta có: \(C\left( x \right) = {x^4} + 4\,{x^2} + 5\).
Vì \({x^4}\, \ge 0\) và \({x^2} \ge 0\) với mọi \(x\) nên \({x^4} + 4{x^2} + 5 > 0\) với mọi \(x\)
Hay \(C\left( x \right) > 0\) với mọi \(x.\)
\( \Rightarrow \) Không có giá trị nào của \(x\) làm cho \(C\left( x \right) = 0\).
\( \Rightarrow \,C\left( x \right)\) là đa thức không có nghiệm.
LG bài 3
Phương pháp giải:
Nếu tại \(x = a\) đa thức \(P\left( x \right)\) có giá trị bằng \(0\) thì ta nói \(a\) là một nghiệm của đa thức \(P\left( x \right)\).
Lời giải chi tiết:
\(\begin{array}{l}a)\,2\,x + 5 = 0\\ \Leftrightarrow 2\,x = - 5\\ \Leftrightarrow \,\,\,\,x\,\, = \dfrac{{ - 5}}{2}\end{array}\)
\( \Rightarrow \) Nghiệm của đa thức \(2\,x + 5 = 0\) là \(x = \dfrac{{ - 5}}{2}.\)
\(b)\,2\,{x^2} + \dfrac{2}{3} = 0\) \( \Leftrightarrow 2\,{x^2} = \dfrac{{ - 2}}{3}\) (Vô lý vì \(2{x^2} \ge 0\) với mọi \(x\) ).
\( \Rightarrow \) Đa thức \(2\,{x^2} + \dfrac{2}{3}\) không có nghiệm.
\(c)\,\left( {x - 7} \right).\left( {{x^2} - \dfrac{9}{{16}}} \right) = 0\).
\( \Leftrightarrow x - 7 = 0\) hoặc \({x^2} - \dfrac{9}{{16}} = 0\).
\( \Leftrightarrow x = 7\) hoặc \({x^2} = \dfrac{9}{{16}}\).
\( \Leftrightarrow x = 7\) hoặc \(x = \pm \,\dfrac{3}{4}\).
Vậy nghiệm của đa thức là \(x = 7\) hoặc \(x = \dfrac{3}{4}\) hoặc \(x = - \dfrac{3}{4}\).
LG bài 4
Phương pháp giải:
a) Chứng minh hai tam giác bằng nhau theo trường hợp c.g.c.
b) Chứng minh \(\Delta ABD\)là tam giác cân có một góc bằng \({60^0}\), rồi suy ra \(\Delta ABD\) là tam giác đều.
c) Chứng minh \(DE = DH\) (hai cạnh tương ứng). Mà \(DH = DB\) (giả thiết) \( \Rightarrow DE = DB\).
d) Chứng minh \(FD//AB\) rồi sau đó chứng minh \(DI//AB\), rồi suy ra \(I,\,D,\,F\) là ba điểm thẳng hàng.
Lời giải chi tiết:
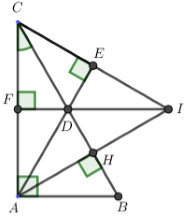
a) Xét \(\Delta AHB\) và \(\Delta AHD\) ta có:
\(HD = HB\) (gt)
\(AH\,\,chung\)
\(\angle AHB = \angle AHD = {90^0}\)
\( \Rightarrow \)\(\Delta AHB = \,\Delta AHD\) (c.g.c)
b) \(\Delta ABC\) vuông tại \(A\), có \(\angle C = {30^0} \)\(\Rightarrow \angle B = {90^0} - {30^0} = {60^0}\) (định lý tổng ba góc của một tam giác).
Vì \(\Delta AHB = \,\Delta AHD\) (cmt)
\( \Rightarrow AB = AD\) (hai cạnh tương ứng).
\( \Rightarrow \Delta ABD\) cân tại \(A\) mà \(\angle B = {60^0}\)
Do đó: \(\Delta ABD\) là tam giác đều.
c) Vì \(\Delta ABD\) là tam giác đều (cmt)
\( \Rightarrow \angle DAB = {60^0}\)
\(\begin{array}{l} \Rightarrow \angle CAD = {90^0} - \angle DAB\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {90^0} - {60^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {30^0}\end{array}\)
Xét \(\Delta ACD\) có \(\angle ACD = \angle \,CAD = {30^0}\).
\( \Rightarrow \Delta ACD\) cân tại \(D.\)
\( \Rightarrow \,CD = AD\)
Xét \(\Delta DEC\) và \(\Delta DHA\) có:
\(CD = AD\,\,\left( {cmt} \right)\)
\(\angle E = \angle H = {90^0}\)
\(\angle CDE = \angle ADH\) (đối đỉnh)
\( \Rightarrow \,\Delta DEC = \Delta DHA\) (cạnh huyền – góc nhọn).
\( \Rightarrow DE = DH\) (hai cạnh tương ứng).
Mà \(DH = HB\) (giả thiết)
\( \Rightarrow DE = HB\).
d) Từ \(D\) kẻ \(DF\) vuông góc với \(AC\) (\(F\,\)thuộc \(AC\)), \(I\) là giao điểm của \(CE\) và \(AH.\) Chứng minh ba điểm \(I,\,D,\,F\) thẳng hàng.
Ta có:
\(\begin{array}{l}DF \bot AC\,\left( {gt} \right)\\AB \bot AC\left( {gt} \right)\\ \Rightarrow DF//AB\,\,\,\,\,\,\,\left( 1 \right)\end{array}\)
Ta lại có:
\(\angle FDC = \angle HDI\) (đối đỉnh)
Mà \(\angle FDC = {90^0} - \angle C = {90^0} - {30^0} = {60^0}\)
\( \Rightarrow \angle FDC = \angle HDI = {60^0}\)
Mà \(\angle B = {60^0}\)
\( \Rightarrow \angle B = \angle HDI\)
Mà hai góc này ở vị trí so le trong
Do đó: \(DI//AB\) (2)
Từ (1) và (2), suy ra: \( I,D,F\) là ba điểm thẳng hàng.
LG bài 5
Phương pháp giải:
Biến đổi \(P(x)=0\) về dạng \(A.B=m\) với \(m\) là số nguyên
Khi đó, lập luận để có \(A,B\in Ư(m)\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}P\left( x \right) = {x^3} - x + 5 = 0\\ \Leftrightarrow {x^3} - x = - 5\\ \Leftrightarrow x\left( {{x^2} - 1} \right) = - 5\end{array}\)
Gọi \(k\) là nghiệm nguyên của đa thức \(P\left( x \right)\)
\( \Rightarrow k\left( {{k^2} - 1} \right) = - 5\).
\( \Rightarrow k \in \,Ư\left( 5 \right) = \left\{ { - 1;1; - 5;5} \right\}\).
Ta có bảng sau:
|
\(k\) |
\( - 1\) |
\(1\) |
\( - 5\) |
\(5\) |
|
\(P\left( x \right)\) |
5 |
5 |
\( - 120\) |
125 |
|
Kết luận |
Loại |
Loại |
Loại |
Loại |
Vậy đa thức \(P\left( x \right)\) không có nghiệm nguyên.
Nguồn sưu tầm
Loigiaihay.com












Danh sách bình luận