Đề kiểm tra giữa kì II Toán 7 - Đề số 4 có lời giải chi tiết
Đề kiểm tra giữa kì 2 toán 7- Đề số 4 có lời giải chi tiết
Đề bài
I. TRẮC NGHIỆM Chọn chữ cái đặt trước câu trả lời đúng:
Câu 1: Điểm thi đua các tháng trong năm học 2013-2014 của lớp 7A được ghi trong Bảng 1:
Tần số của điểm 8 là:
A.12 ; 1 và 4 B. 3
C. 8 D. 10
Câu 2: Mốt của dấu hiệu điều tra trong bảng 1 là :
A. 3 B. 8
C. 9 D. 10
Câu 3: Đơn thức nào sau đây đồng dạng với đơn thức \( - 3x{y^2}\)
A. \( - 3{x^2}y\) B. \(\left( { - 3xy} \right)y\)
C. \( - 3{\left( {xy} \right)^2}\) D. \( - 3xy\)
Câu 4: Kết quả của phép tính \( - 5{x^2}{y^5} - {x^2}{y^5} + 3{x^2}{y^5}\)
A. \( - 3{x^2}{y^5}\) B. \(8{x^2}{y^5}\)
C. \(4{x^2}{y^5}\) D. \( - 4{x^2}{y^5}\)
Câu 5: Giá trị của biểu thức \(3{x^2}y + 3{x^2}y\) tại \(x = {\rm{\;}} - 2\) và \(y = {\rm{\;}} - 1\) là:
A. 12 B. \( - 9\)
C. 18 D. \( - 24\)
Câu 6: Tam giác có một góc \({60^0}\) thì với điều kiện nào thì trở thành tam giác đều :
A. ba góc nhọn
B. hai cạnh bằng nhau
C. hai góc nhọn
D. một cạnh đáy
Lời giải chi tiết
I. TRẮC NGHIỆM
|
1.B |
2.B |
3.B |
4.A |
|
5.D |
6.B |
7.1.A |
7.2.D |
Câu 1 (NB)
Phương pháp: Số lần xuất hiện của một giá trị trong dãy các giá trị của dấu hiệu là tần số của giá trị đó.
Quan sát bảng số liệu, đếm xem điểm 8 xuất hiện bao nhiêu lần ? số điểm 8 chính là tần số của điểm 8.
Cách giải:
Trong bảng 1, điểm 8 xuất hiện 3 lần.
Vậy tần số của điểm 8 là 3.
Chọn B
Câu 2 (NB)
Phương pháp: Mốt của dấu hiệu là giá trị có tần số lớn nhất.
Cách giải:
trong bảng 1 ta thấy điểm 8 xuất hiện với tần số lớn nhất là 3.
Vậy mốt của dấu hiệu là : điểm 8
Chọn B
Câu 3 (TH)
Phương pháp: Hai đơn thức đồng dạng là hai đơn thức có cùng hệ số, nhưng khác phần biến.
Cách giải:
Đơn thức khác hệ số và có cùng phần biến với đơn thức \( - 3x{y^2}\)là: \(\left( { - 3xy} \right)y = {\rm{\;}} - 3x{y^2}\)
Chọn B
Câu 4 (TH)
Phương pháp: Cộng các đơn thức đồng dạng, ta cộng phần hệ số với nhau và giữ nguyên phần biến.
Cách giải:
Ta có: \( - 5{x^2}{y^5} - {x^2}{y^5} + 3{x^2}{y^5} = \left( { - 5 - 1 + 3} \right){x^2}{y^5} = {\rm{\;}} - 3{x^2}{y^5}\)
Chọn A.
Câu 5 (TH) Phương pháp: Thu gọn đa thức rồi thay giá trị của x , y vào.
Cách giải:
Thu gọn đa thức ta được: \(3{x^2}y + 3{x^2}y = 6{x^2}y\)
Thay \(x = {\rm{\;}} - 2;{\mkern 1mu} y = {\rm{\;}} - 1\) vào biểu thức đã được thu gọn ta có: \(6.{\left( { - 2} \right)^2}\left( { - 1} \right) = {\rm{\;}} - 24\)
Chọn D
Câu 6 (TH)
Phương pháp: Ta có:Tam giác cân có 1 góc bằng \({60^0}\)là tam giác đều.
Cách giải:
Tam giác có một góc bằng \({60^0}\)và có hai cạnh bằng nhau là tam giác đều.
Chọn B
Câu 7 (VD)
1) Phương pháp:
Lập bảng tần số theo bảng thống kê ban đầu.
Bước 1: Liệt kê các giá trị không trùng nhau.
Bước 2: Đếm số lần xuất hiện của mỗi giá trị đó. Rồi sắp xếp các số liệu tương ứng vào bảng.
Tìm mốt của dấu hiệu: là giá trị có tần số lớn nhất trong bảng tần số. Dựa trên bảng tần số và giá trị trung bình, đưa ra nhận xét.
Cách giải:
+ Bảng tần số:
+ Mốt của dấu hiệu là:
\({M_0} = 80\)
Chọn A
2) Phương pháp:
Điểm trung bình: Dựa vào bảng tần số, ta có thể tính số trung bình cộng của một dấu hiệu (gọi tắt là số trung bình cộng và kí hiệu là \(\bar X\) ) như sau :
+ Nhân từng giá trị với tần số tương ứng.
+ Cộng tất cả các tích vừa tìm được.
+ Chia tổng đó cho số các giá trị (tức tổng các tần số).
Ta có công thức : \(\bar X{\rm{\;}} = \frac{{{x_1}{n_1} + {x_2}{n_2} + {x_3}{n_3} + ... + {x_k}{n_k}}}{{\rm{N}}}\)
Trong đó : \({x_1},{\mkern 1mu} {x_2},{\mkern 1mu} ....,{\mkern 1mu} {x_k}\) là k giá trị khác nhau của dấu hiệu X.
\({n_1},{\mkern 1mu} {n_2},...,{n_k}\) là k tần số tương ứng.
N là số các giá trị.
Cách giải:
Số điểm trung bình thi đua của lớp 7A là :
\(\overline {X{\mkern 1mu} } {\rm{\;}} = \frac{{70.2 + 90.2 + 80.5}}{9} = 80\)
Chọn D
Câu 8 (VD) Phương pháp:
1) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh-góc-cạnh.
2) Chứng minh hai góc ở đáy của tam giác bằng nhau.
3) Áp dụng tính chất tam giác cân, đường trung tuyến và bất đẳng thức tam giác để chứng minh.
Cách giải:
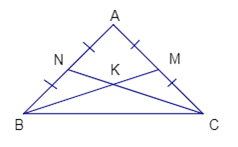
1) Xét \(\Delta BNC\) và \(\Delta CMB\) có:
\(\begin{array}{*{20}{l}}{BN = AN = \frac{{AB}}{2};{\mkern 1mu} }\\{CM = AM = \frac{{AC}}{2};}\\{AB = AC}\end{array}\)
\( \Rightarrow BN = CM\)
\(\angle B = \angle C\) (\(\Delta ABC\) cân tại A)
BC cạnh chung.
Do đó: \(\Delta BNC = \Delta CMB\left( {c.g.c} \right)\)
2) Chứng minh: \(\Delta KBC\) cân tại K.
Do \(\Delta BNC = \Delta CMB\left( {cmt} \right)\)
\( \Rightarrow \angle MBC = \angle NCB\)(hai góc tương ứng)
\( \Rightarrow \Delta KBC\) cân tại K.
3) Chứng minh \(BC < 4KM\)
Ta có: \(\Delta KBC\) cân tại K. (cmt)
\( \Rightarrow BK = CK\)
Ta có : \(BK + CK = BK + BK = 2BK = 2.2KM = 4KM\) (tính chất đường trung tuyến).
Mà \(\Delta KBC\) có : \(KB + KC > BC\) (bất đẳng thức tam giác)
Suy ra \(BC < 4.KM\) (đpcm).
















Danh sách bình luận