Đề kiểm tra giữa kì I Toán 7 - Đề số 4 có lời giải chi tiết
Đề kiểm tra giữa kì I Toán 7 - Đề số 4 có lời giải chi tiết
Đề bài
Câu 1 (2,5 điểm):
1) Thực hiện phép tính:
a) \(\frac{2}{5} + \frac{3}{5} \cdot \left( {\frac{{ - 4}}{9}} \right)\)
b) \(3 - {\left( { - 0,75} \right)^0} + {\left( { - 0,5} \right)^2}:2\)
2) Làm tròn số 17,418 đến chữ số thập phân thứ hai.
Câu 2 (2 điểm): Tìm \(x\), biết:
a) \(\frac{1}{2} + x = \frac{1}{4}\)
b) \( - 0,52:x = - 9,36:16,38\)
Câu 3 (2 điểm): Số học sinh ba lớp 7A, 7B, 7C tỉ lệ với 4; 5; 6 và tổng số học sinh của ba lớp là 105 học sinh. Tính số học sinh mỗi lớp.
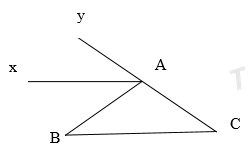
Câu 4 (3 điểm): Cho tam giác \(ABC\) có \(\widehat B = \widehat C = {40^0}\).
a) Tính số đo \(\widehat {BAC}\)
b) Gọi \(Ax\) là tia phân giác của góc ngoài ở đỉnh \(A\). Hãy chứng tỏ rằng \(Ax{\rm{ }}//{\rm{ }}BC.\)
Câu 5 (0,5 điểm): Tìm giá trị nhỏ nhất của biểu thức
\(A = \left| {x - 1} \right| + \left| {x + 2012} \right|\)\(\)
Lời giải chi tiết
Câu 1:
Phương pháp:
1) a, Thực hiện phép tính theo thứ tự nhân chia trước, cộng trừ sau.
b, Thực hiện phép tính với lũy thừa trước, sau đó thực hiện ưu tiên nhân chia trước, cộng trừ sau.
2) Vận dụng quy tắc làm tròn số.
Cách giải:
1) a) \(\frac{2}{5} + \frac{3}{5} \cdot (\frac{{ - 4}}{9})\) = \(\frac{2}{5} + \left( { - \frac{4}{{15}}} \right)\)
= \(\frac{6}{{15}} + \left( { - \frac{4}{{15}}} \right)\) = \(\frac{2}{{15}}\)
b) \(3 - {\left( { - 0,75} \right)^0} + {\left( { - 0,5} \right)^2}:2\) = \(3 - 1 + 0,25:2\) = 2,125
2) 17,418 \( \approx \)17,42
Câu 2:
Phương pháp:
a) Thực hiện tìm số chưa biết, rồi vận dụng quy tắc cộng trừ nhân chia số hữu tỉ để tính.
b) Thực hiện tính vế phải, sau đó tìm số chưa biết bằng cách vận dụng quy tắc cộng trừ nhân chia số hữu tỉ.
Cách giải:
|
a. \(\frac{1}{2} + x = \frac{1}{4}\) \(x = \frac{1}{4} - \frac{1}{2}\) \(x = - \frac{1}{4}\) Vậy \(x = - \frac{1}{4}\). |
b. \( - 0,52:x = - 9,36:16,38\) \( \Rightarrow x \cdot ( - 9,36) = ( - 0,52) \cdot 16,38\) \(x = \frac{{( - 0,52) \cdot 16,38}}{{ - 9,36}}\) \(x = 0,91\) Vậy \(x = 0,91\). |
Câu 3:
Phương pháp:
Áp dụng tính chất của dãy tỉ số bằng nhau để tìm ra số học sinh của mỗi lớp.
Cách giải:
Gọi số học sinh của ba lớp 7A,7B,7C lần lượt là: a,b,c (học sinh) ( a,b,c \( \in \)N*)
Theo đề bài ta có:\(\frac{a}{4} = \frac{b}{5} = \frac{c}{6}\) và a + b + c = 105
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{4} = \frac{b}{5} = \frac{c}{6} = \frac{{a + b + c}}{{4 + 5 + 6}} = \frac{{105}}{{15}} = 7\)
Suy ra:
\(\begin{array}{l}\frac{a}{4} = 7 \Rightarrow a = 28\\\frac{b}{5} = 7 \Rightarrow b = 35\\\frac{c}{6} = 7 \Rightarrow c = 42\end{array}\)
Vậy số học sinh của ba lớp 7A,7B,7C lần lượt là 28,35,42 (Học sinh).
Câu 4:
Phương pháp:
a) Dựa vào định lý tổng ba góc của một tam giác.
b) Vận dụng định lý góc ngoài của một tam giác để tính góc \(\angle BAy\), sau đó chỉ ra \(\widehat {ABC}\)= \(\widehat {BAx}\) = 400 , mà hai góc này ở vị trí so le trong, do đó: Ax // BC.
Cách giải:
a) \(\Delta \)ABC có \(\widehat {BAC}\)+\(\widehat B\)+\(\widehat C\)= 1800 ( Định lí tổng ba góc của một tam giác)
\( \Rightarrow \) \(\widehat {BAC}\) = 1000.
b) \(\widehat {BAy}\) là góc ngoài của tam giác ABC
=>\(\widehat {BAy}\)= \(\widehat B\)+\(\widehat C\) ( Định lí góc ngoài của tam giác)
=> \(\widehat {BAy}\)= 800.
Vì Ax là tia phân giác của góc \(\widehat {BAy}\)
=> \(\widehat {BAx}\)= \(\widehat {xAy}\)= \(\widehat {BAy}\) : 2 = 400
Ta có \(\widehat {ABC}\)= \(\widehat {BAx}\) = 400
Mà \(\widehat {ABC}\) và \(\widehat {BAx}\) là hai góc ở vị trí so le trong
=>Ax // BC.
Câu 5:
Phương pháp: Áp dụng: \(\left| a \right| + \left| b \right| \ge \left| {a + b} \right|\) , từ đó lập luận tìm ra giá trị nhỏ nhất của biểu thức \(A.\)
Cách giải:
Ta có: \(A = \left| {x - 1} \right| + \left| {x + 2012} \right| = \left| {1 - x} \right| + \left| {x + 2012} \right|\)
\( \ge \left| {1 - x + x + 2012} \right| = 2013\)
Dấu “=” xảy ra khi \((1 - x)(x + 2012) \ge 0 \Leftrightarrow - 2012 \le x \le 1\)
Kết luận: Giá trị nhỏ nhất của \(A\) là 2013 tại \( - 2012 \le x \le 1\).
- Đề kiểm tra giữa kì I Toán 7 - Đề số 5 có lời giải chi tiết
- Đề kiểm tra giữa kì I Toán 7 - Đề số 6 có lời giải chi tiết
- Đề kiểm tra giữa kì I Toán 7 - Đề số 7 có lời giải chi tiết
- Đề kiểm tra giữa kì I Toán 7 - Đề số 3 có lời giải chi tiết
- Đề kiểm tra giữa kì I Toán 7 - Đề số 1 có lời giải chi tiết
>> Xem thêm













Danh sách bình luận