Đề cương ôn tập học kì 1 toán 7

LT đại số

I. Số hữu tỉ và số thực

1) Số hữu tỉ

Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}\) với a, b \( \in \mathbb{Z}\) , b \( \ne \)0.

2) Cộng, trừ, nhân, chia số hữu tỉ.

Với x = \(\frac{a}{m}\) ; y = \(\frac{b}{m}\)

Với x = \(\frac{a}{b}\) ; y = \(\frac{c}{d}\)

\(\begin{array}{l}x + y = \frac{a}{m} + \frac{b}{m} = \frac{{a + b}}{m}\\x - y = \frac{a}{m} - \frac{b}{m} = \frac{{a - b}}{m}\end{array}\)

3) Tính chất của dãy tỉ số bằng nhau.

\(\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = \frac{{a + c + e}}{{b + d + f}} = \frac{{a - c + e}}{{b - d + f}} = \frac{{a - c}}{{b - d}} = ...\)(giả thiết các tỉ số đều có nghĩa)

4) Một số quy tắc ghi nhớ khi làm bài tập

a) Quy tắc bỏ ngoặc:

Bỏ ngoặc trước ngoặc có dấu “-” thì đồng thời đổi dấu tất cả các hạng tử có trong ngoặc, còn trước ngoặc có dấu “+” thì vẫn giữ nguyên dấu các hạng tử trong ngoặc.

b/ Quy tắc chuyển vế: Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó.

Với mọi \(x,y,\,z \in Q\) : \(x + y = z \Rightarrow x = z – y\)

5) Giá trị tuyệt đối của một số hữu tỉ:

Định nghĩa: Giá trị tuyệt đối của một số hữu tỉ x, kí hiệu \(\left| x \right|\) là khoảng cách từ điểm x tới điểm 0 trên trục số.

6) Lũy thừa của một số hữu tỉ

a) Định nghĩa: \({x^n} = \underbrace {x.x.x...x}_{n thừa số x }\)\((x \in Q,\,n \in N,\,n > 1)\)

Quy ước: x¹ = x; x⁰ = 1 (\(x \ne 0\))

b) Tích và thương của hai lũy thừa cùng cơ số

\({x^m}.{x^n} = {x^{m + n}}\) \({x^m}:{x^n} = {x^{m - n}}\)( \(x \ne 0\), \(m \ge n\))

c) Lũy thừa của lũy thừa \({\left( {{x^m}} \right)^n} = {x^{m.n}}\)

d) Lũy thừa của một tích, lũy thừa của một thương

\({\left( {x.y} \right)^n} = {x^n}.{y^n}\) \({\left( {x:y} \right)^n} = {x^n}:{y^n}\)(\(y \ne 0\))

Chú ý: Với \(a \ne 0\), a \( \pm 1\), nếu a^m = aⁿ thì m = n

II. Hàm số và đồ thị:

1. Đại lượng tỉ lệ thuận

a) Định nghĩa: y = kx (k\( \ne \)0)

b)Tính chất:

Tính chất 1: \(\frac{{{y_1}}}{{{x_1}}} = \frac{{{y_2}}}{{{x_2}}} = \frac{{{y_3}}}{{{x_3}}} = ... = k\)

Tính chất 2: \(\frac{{{x_1}}}{{{x_2}}} = \frac{{{y_1}}}{{{y_2}}};\,\,\,\,\,\,\,\,\frac{{{x_3}}}{{{x_4}}} = \frac{{{y_3}}}{{{y_4}}};....\)

2. Đại lượng tỉ lệ nghịch

a) Định nghĩa: y = \(\frac{a}{x}\) (a\( \ne \)0) hay x.y =a

b)Tính chất:

Tính chất 1: \({x_1}.{y_1} = {x_2}.{y_2} = {x_3}.{y_3} = ... = a\)

Tính chất 2: \(\frac{{x{}_1}}{{{x_2}}} = \frac{{{y_2}}}{{{y_1}}};\,\,\,\,\,\,\,\frac{{{x_3}}}{{{x_4}}} = \frac{{{y_4}}}{{{y_3}}};......\)

3. Khái niệm hàm số:

Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x.

Kí hiệu y =f(x) hoặc y = g(x) … và x được gọi là biến số.

4. Đồ thị hàm số y = f(x):

Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng(x ; y) trên mặt phẳng tọa độ.

Đồ thị hàm số y = ax (a\( \ne \)0) là một đường thẳng đi qua gốc tọa độ.

LT hình học

I. Đường thẳng vuông góc, đường thẳng song song

1. Hai góc đối đỉnh

- Định nghĩa hai góc đối đỉnh: Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

- Định lí về hai góc đối đỉnh: Hai góc đối đỉnh thì bằng nhau.

2. Hai đường thẳng vuông góc:

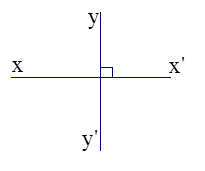
- Hai đường thẳng xx’, yy’ cắt nhau và trong các góc tạo thành có một góc vuông được gọi là hai đường thẳng

vuông góc và được kí hiệu là xx’\( \bot \)yy’.

- Đường trung trực của đường thẳng: Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng ấy.

3. Dấu hiệu nhận biết hai đường thẳng song song:

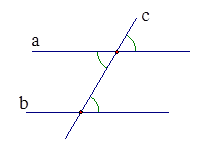
Nếu đường thẳng c cắt hai đường thẳng a,b và trong các

góc tạo thành có một cặp góc so le trong bằng nhau

(hoặc một cặp góc đồng vị bằng nhau) thì a và b

song song với nhau (a // b)

4. Tiên đề Ơ-clit: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.

5. Tính chất hai đường thẳng song song:

Nếu một đường thẳng cắt hai đường thẳng song song thì:

a) Hai góc so le trong bằng nhau

b) Hai góc đồng vị bằng nhau

c) Hai góc trong cùng phía bù nhau.

II. Tam giác

1. Tổng ba góc của tam giác:

- Tổng ba góc của một tam giác bằng 180⁰.

- Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.

2. Định nghĩa hai tam giác bằng nhau

Định nghĩa: Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

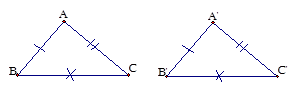
3. Trường hợp bằng nhau thứ nhất của tam giác (cạnh – cạnh – cạnh).

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

\(\Delta ABC = \Delta A'B'C'\)(c.c.c)

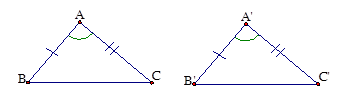
4. Trường hợp bằng nhau thứ hai của tam giác (cạnh – góc – cạnh).

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

\(\Delta ABC = \Delta A'B'C'\)(c.g.c)

5. Trường hợp bằng nhau thứ ba của tam giác (góc – cạnh – góc).

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

\(\Delta ABC = \Delta A'B'C'\)(g.c.g)

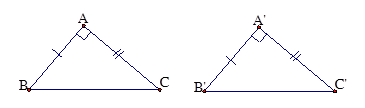
6. Trường hợp bằng nhau thứ nhất của tam giác vuông: (hai cạnh góc vuông)

Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

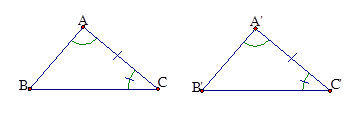
7. Trường hợp bằng nhau thứ hai của tam giác vuông: (cạnh huyền - góc nhọn)

Nếu cạnh huyền và góc nhọn của tam giác vuông này bằng cạnh huyền và góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

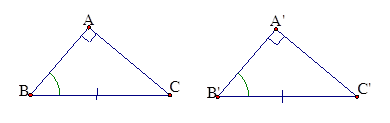
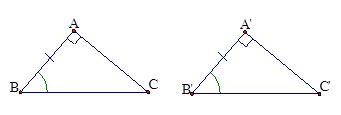
8. Trường hợp bằng nhau thứ ba của tam giác vuông: (cạnh góc vuông - góc nhọn kề)

Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

9. Tam giác cân

- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau

- Trong một tam giác cân, hai góc ở đáy bằng nhau

- Nếu một tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân

- Tam giác vuông cân là tam giác có 2 cạnh góc vuông bằng nhau. Mỗi góc nhọn của tam giác vuông cân bằng 45 độ

10. Tam giác đều

- Định nghĩa: Tam giác đều là tam giác có ba cạnh bằng nhau

- Mỗi góc của tam giác đều bằng 60 độ

- Nếu một tam giác có ba cạnh bằng nhau thì tam giác đó là tam giác đều

- Nếu một tam giác cân có một góc bằng 60 độ thì tam giác đó là tam giác đều

Các cách chứng minh thường được áp dụng trong chương trình Toán 7:

1/ Để chứng minh 2 góc bằng nhau: Ta thường chứng minh :

+ 2 góc đó là 2 góc tương ứng của 2 tam giác bằng nhau.

+ 2 góc đó là 2 góc so le trong, 2 góc đồng vị của 2 đường thẳng song song.

2/ Để chứng minh 2 đoạn thẳng bằng nhau:

Ta thường chứng minh: Hai đoạn thẳng đó là 2 cạnh tương ứng của 2 tam giác bằng nhau.

3/ Chứng minh song song

Chứng minh 2 góc so le trong bằng nhau.

Chứng minh 2 góc đồng vị bằng nhau.

Chứng minh 2 góc trong cùng phía bù nhau.

Chứng minh 2 đường thẳng cùng song song với đường thẳng thứ 3.

Chứng minh 2 đường thẳng cùng vuông góc với đường thẳng thứ 3.

4/ Chứng minh tia phân giác:

Chứng minh 2 góc đó bằng nhau.

5/ Chứng minh vuông góc:

+ Chứng minh góc tạo bởi hai đường thẳng đó bằng 90⁰.

(Chứng minh 2 góc bằng nhau, mà tổng 2 góc đó lại bằng 180⁰ => mỗi góc = 90⁰)

+ Chứng minh vuông góc với 1 trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.

BT trắc nghiệm

I. Trắc nghiệm

Câu 1: Nếu \(\sqrt x = 9\) thì \(x = \)?

a. \(x = 3\); b. \(x = - 3\); c. \(x = 81\); d. \(x = - 81\)

Câu 2: Cho \(\frac{{12}}{x} = \frac{4}{9}\) .Giá trị của \(x\)là:

a. \(x = 3\); b. \(x = - 3\); c. \(x = 27\); d. \(x = - 27\)

Câu 3: Khẳng định nào sau đây đúng:

a. \({\left( { - 2} \right)^8} = - {2^8}\); b. \({\left( {\frac{{ - 2}}{3}} \right)^3} = \frac{{ - 6}}{9}\);

c. \({\left( {\frac{{ - 1}}{2}} \right)^4} = \frac{1}{{16}}\); d. \({\left[ {{{\left( { - 2} \right)}^3}} \right]^2} = {2^5}\)

Câu 4: Cho 3 đường thẳng m,n,p. Nếu m//n, p\( \bot \)n thì:

a. m//p; b. m\( \bot \)p; c. n//p; d. m\( \bot \)n.

Câu 5: Khẳng định nào sau đây đúng:

Hai góc bằng nhau thì đối đỉnh.
Hai góc đối đỉnh thì bù nhau.
Hai góc đối đỉnh thì phụ nhau.
Hai góc đối đỉnh thì bằng nhau.

Câu 6: Cho và \(\Delta MNP\), biết: \(\widehat A = \widehat M\), \(\widehat B = \widehat N\). Để \(\Delta ABC = \Delta MNP\) theo trường hợp góc – cạnh – góc (g-c-g) thì cần thêm yếu tố nào:

a. \(AB = MN\); b. \(AB = MP\);

c. \(AC = MN\); d. \(BC = MP\).

Câu 7: Khẳng định nào sau đây là đúng:

a. \(0,2\left( 5 \right) \in I\); b. \(\sqrt {25} \in I\).;

c. \( - \sqrt 9 \in \mathbb{R}\); d. \(3,4 \in \mathbb{Q}\)

Câu 8: Chọn câu đúng: \(\left| x \right| = \frac{5}{7}\)

a. \(x = - \frac{5}{7}\); b. \(x = \frac{5}{7}\);

c. c. \(x = \frac{5}{7}\) hoặc \(x = - \frac{5}{7}\); d. Tất cả đều sai.

Câu 9: Cho 3 đường thẳng e,d,f. Nếu e//d,e//f thì:

a. d//f. b. d\( \bot \)f.

c. Hai câu a và b đều đúng. d. Hai câu a và b đều sai.

Câu 10: Khẳng định nào sau đây là sai:

Một tam giác chỉ có thể có một góc vuông.
Một tam giác có thể có ba góc nhọn.
Trong một tam giác chỉ có thể có nhiều nhất 1 góc tù.
Trong tam giác vuông, hai góc nhọn bù nhau.

Câu 11: Nếu \(\sqrt a = 4\) thì \({a^2}\) bằng:

a. 2; b. 4; c. 8; d. 16.

Câu 12: Kết quả của phép tính \({2^8}:{2^2}\) là:

a. \({2^{10}}\); b. \({2^6}\); c. \({2^{16}}\); d. \({2^4}\).

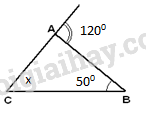
Câu 13: Cho hình vẽ sau, tìm x:

a. \(x = {120^0}\)

b. \(x = {50^0}\)

c. \(x = {70^0}\)

d. \(x = {170^0}\)

Câu 14: Giá trị của biểu thức A=\({\left( {5 + {2^3} - {3^2}} \right)^0}\)là:

a. A = 2; b. A = 4; c. A = 0; d. A = 1.

Câu 15: Kết quả của phép tính \(\left| 3 \right| - \left| { - 2} \right|\) là:

a. 5; b.\( - \)5; c. \( - \)1; d. 1 .

Câu 16: Cho biết \(\sqrt x = 9\), khi đó \(\left| x \right|\) là:

a. \(3\); b.\( - 3\); c. 81; d.\( - \)81.

Câu 17: Khẳng định nào sau đây đúng:

a. 25,6754 > 25,7; b. – 6,78546 > – 6, 77656 ;

c. \( - \)0,2176 > \( - \)0,2276; d. 0,2(314) = 0,2314.

Câu 18: Cho tam giác ABC có :\(\widehat A = {60^0}\) và \(\widehat B = 2\widehat C\), khi đó số đo của góc B và C là:

a. \(\widehat B = {100^0},\widehat C = {50^0}\); b. \(\widehat B = {120^0},\widehat C = {60^0}\);

c. \(\widehat B = {80^0},\widehat C = {40^0}\); d. \(\widehat B = {60^0},\widehat C = {30^0}\)

Câu 19: Cho \(\Delta ABC\) và \(\Delta PMN\) bằng nhau có: AB=PN; CB=PM; \(\widehat B = \widehat P\), khi đó cách viết nào sau đây đúng:

a. \(\Delta ABC = \Delta PNM\); b. \(\Delta BAC = \Delta PNM\);

c. \(\Delta CAB = \Delta NMP\); d. \(\Delta BCA = \Delta MNP\)

BT tự luận đại số

Dạng 1: Thực hiện phép tính

1) \(\frac{3}{7} + \left( { - \frac{5}{2}} \right) + \left( { - \frac{3}{5}} \right)\)

2) \(\frac{{ - 8}}{{18}} - \frac{{15}}{{27}}\)

3) \(\frac{4}{5} - \left( { - \frac{2}{7}} \right) - \frac{7}{{10}}\)

5) \(3,5 - \left( { - \frac{2}{7}} \right)\)

6) \(\left( { - 3} \right).\left( { - \frac{7}{{12}}} \right)\)

7) \(\left( {\frac{{11}}{{12}}:\frac{{33}}{{16}}} \right).\frac{3}{5}\)

8) \(\sqrt {{{( - 7)}^2}} + \sqrt {\frac{{25}}{{16}}} - \frac{3}{2}\)

9) \(\frac{1}{2}.\sqrt {100} - \sqrt {\frac{1}{{16}}} + {(\frac{1}{3})^0}\)

10) \(\left( {\frac{9}{{25}} - 2.18} \right):\left( {3\frac{4}{5} + 0,2} \right)\)

11) \(\frac{3}{8}.19\frac{1}{3} - \frac{3}{8}.33\frac{1}{3}\)

12) \(\frac{4}{{23}} + \frac{5}{{21}} - \frac{4}{{23}} + 0,5 + \frac{{16}}{{21}}\)

13) \(\frac{{21}}{{47}} + \frac{9}{{45}} + \frac{{26}}{{47}} + \frac{4}{5}\)

14) \(\frac{{15}}{{12}} + \frac{5}{{13}} - \frac{3}{{12}} - \frac{{18}}{{13}}\)

15) \(\frac{{13}}{{25}} + \frac{6}{{41}} - \frac{{38}}{{25}} + \frac{{35}}{{41}} - \frac{1}{2}\)

16) \(12.{\left( { - \frac{2}{3}} \right)^2} + \frac{4}{3}\)

17) \(12,5.\left( { - \frac{5}{7}} \right) + 1,5.\left( { - \frac{5}{7}} \right)\)

18) \(\frac{4}{5}.{\left( {\frac{7}{2} + \frac{1}{4}} \right)^2}\)

19) \(3 - {\left( { - \frac{6}{7}} \right)^0} + {\left( {\frac{1}{2}} \right)^2}:2\)

20) \({\left( { - 2} \right)^3} + {2^2} + {\left( { - 1} \right)^{20}} + {\left( { - 2} \right)^0}\,\,\)

21) \({\left( {{{\left( 3 \right)}^2}} \right)^2} - {\left( {{{\left( { - 5} \right)}^2}} \right)^2} + {\left( {{{\left( { - 2} \right)}^3}} \right)^2}\,\,\,\,\)

22) \({2^4} + 8{\left[ {{{\left( { - 2} \right)}^2}:\frac{1}{2}} \right]^0} - {2^{ - 2}} \cdot 4 + {\left( { - 2} \right)^2}\)

23) \({2^3} + 3{\left( {\frac{1}{2}} \right)^0} - {2^{ - 2}} \cdot 4 + \left[ {{{\left( { - 2} \right)}^2}:\frac{1}{2}} \right] \cdot 8\)

Dạng 2: Tìm x

1) \(\frac{4}{5} - x = \frac{1}{3}\)

2) \( - x - \frac{2}{3} = - \frac{6}{7}\)

3) \(\left| {x - \frac{4}{5}} \right| = \frac{3}{4}\)

4) \(6 - \left| {\frac{1}{2} - x} \right| = \frac{2}{5}\)

5) \(\left| {x + \frac{3}{5}} \right| - \frac{1}{2} = \frac{1}{2}\)

6) \(2 - \left| {x - \frac{2}{5}} \right| = - \frac{1}{2}\)

7) \(0,2 + \left| {x - 2,3} \right| = 1,1\)

8) \( - 1 + \left| {x + 4,5} \right| = - 6,2\)

9) \(\left( {\frac{2}{3}x - 1} \right)\left( {\frac{3}{4}x + \frac{1}{2}} \right) = 0\)

10) \({\left( { - \frac{2}{3}} \right)^2}.x = {\left( { - \frac{2}{3}} \right)^5};\)

11) \({\left( {{\rm{x}}\,{\rm{ - }}\,\frac{{\rm{1}}}{{\rm{2}}}} \right)^{\rm{3}}}{\rm{ = }}\frac{{\rm{1}}}{{{\rm{27}}}}{\rm{ }}\)

12) \({\left( {x\, + \,\frac{1}{2}} \right)^2}\, = \,\frac{4}{{25}}\)

13) \({2^{x - 1}} = 16\)

14) \({\left( {x - 1} \right)^{x + 2}} = {\left( {x - 1} \right)^{x + 6}}\)

15) \({\left( {x + 20} \right)^{100}} + \left| {y + 4} \right| = 0\)

Dạng 3: Toán về hai đại lượng tỉ lệ

Bài 1: Cho hai đại lượng x và y tỉ lệ thuận với nhau và khi x = 3 thì y = - 6.

a) Tìm hệ số tỉ lệ k của y đối với x;

b) Hãy biểu diễn y theo x;

c) Tính giá trị y khi x = 1; x = 2.

Bài 2: Cho x và y là hai đại lượng tỉ lệ thuận và x₁ + x₂ = 5; y₁ + y₂ = 10

Hãy biểu diễn y theo x

Bài 3: Cho x và y là hai đại lượng tỉ lệ nghịch với nhau khi x nhận các giá trị x₁ = 3; x₂ = 2 thì tổng các giá trị tương ứng của y là 15 .

a) Hãy biểu diễn y theo x.

b) Tìm giá trị của x khi y = - 6

Bài 4: Cho x và y là hai đại lượng tỉ lệ nghịch khi x₁ = 2; x₂ = 5 thì 3y₁ + 4y₂ = 46

a) Hãy biểu diễn x theo y;

b) Tính giá trị của x khi y = 23

Bài 5: Cho hai đại lượng x và y tỉ lệ nghịch với nhau và khi x = 2 thì y = 4.

a) Tìm hệ số tỉ lệ a;

b) Hãy biểu diễn x theo y;

c) Tính giá trị của x khi y = -1 ; y = 2.

Bài 6: Học sinh ba lớp 7 phải trồng và chăm sóc 24 cây xanh, lớp 7A có 32 học sinh, lớp 7B có 28 học sinh, lớp 7C có 36 học sinh. Hỏi mỗi lớp phải trồng và chăm sóc bao nhiêu cây xanh, biết số cây tỉ lệ với số học sinh.

Bài 7: Biết các cạnh tam giác tỉ lệ với 2:3:4 và chu vi của nó là 45cm. Tính các cạnh của tam giác đó.

Bài 8: Ba đội máy san đất làm ba khối lượng công việc như nhau. Đội thứ nhất hoàn thành công việc trong 3 ngày, đội thứ hai hoàn thành công việc trong 4 ngày, đội thứ ba hoàn thành công việc trong 6 ngày. Hỏi mỗi đội có bao nhiêu máy(có cùng năng suất). Biết rằng đội thứ nhất nhiều hơn đội thứ hai 2 máy ?

Bài 9: Ba đơn vị kinh doanh góp vốn theo tỉ lệ 3; 5; 7. Hỏi mỗi đơn vị sau một năm được chia bao nhiêu tiền lãi? Biết tổng số tiền lãi sau một năm là 225 triệu đồng và tiền lãi được chia tỉ lệ thuận với số vốn đã góp.

Bài 10: Tam giác ABC có số đo các góc A,B,C lần lượt tỉ lệ với 3:4:5. Tính số đo các góc của tam giác ABC.

Bài 11: Tính độ dài các cạnh của tam giác ABC, biết rằng các cạnh tỉ lệ với 4:5:6 và chu vi của tam giác ABC là 30cm

Bài 12: Số học sinh giỏi, khá, trung bình của khối 7 lần lượt tỉ lệ với 2:3:5. Tính số học sinh khá, giỏi, trung bình, biết tổng số học sinh khá và học sinh trung bình hơn học sinh giỏi là 180 em

Bài 13: Ba lớp 8A, 8B, 8C trồng được 120 cây. Tính số cây trồng được của mỗi lớp, biết rằng số cây trồng được của mỗi lớp lần lượt tỉ lệ với 3 : 4 : 5

Bài 14: Ba lớp 7A, 7B, 7C trồng được 90 cây . Tính số cây trồng được của mỗi lớp, biết rằng số cây trồng được của mỗi lớp lần lượt tỉ lệ với 4 : 6 : 8

Bài 15: Tìm số đo mỗi góc của tam giác ABC biết số đo ba góc có tỉ lệ là 1:2:3. Khi đó tam giác ABC là tam giác gì?

Bài 16: Hai thanh kim loại nặng bằng nhau và có khối lượg riêng tương ứng là 3g/cm³ và 5g/cm³. Thể tích của mỗi thanh kim loại nặng bao nhiêu biết tổng thể tích của chúng là 8000cm³.

Bài 17: Một ô tô chạy từ A đến B với vận tốc 45km/h hết 3 giờ 15 phút. Hỏi chiếc xe đó chạy từ A đến B với vận tốc 65 km/h hết bao nhiêu thời gian?

Bài 18: Cho biết 5 người làm cỏ một cánh đồng hết 8 giờ, hỏi 8 người với (cùng năng suất như thế) làm cỏ cánh đồng hết bao nhiêu giờ?

Bài 19: Ba đội máy cày, cày ba cánh đồng cùng diện tích. Đội thứ nhất cày xong trong 3 ngày, đội thứ hai cày xong trong 5 ngày, đội thứ ba cày xong trong 6 ngày. Hỏi mỗi đội có bao nhiêu máy, biết rằng đội thứ ba có ít hơn đội thứ hai 1 máy?

Bài 20: Hai thanh sắt và chì có khối lượng bằng nhau. Hỏi thanh nào có thể tích lớn hơn và lớn hơn bao nhiêu lần ,biết rằng khối lượng riêng của sắt là 7,8 (g/cm³) và của chì là 11,3 (g/cm³)

Dạng 4: Hàm số và đồ thị

Bài 1: Vẽ đồ thị của các hàm số sau trên cùng một hệ trục tọa độ:\({\rm{y = }} - {\rm{2x \,\text{và}\, }}y = - \frac{3}{4}x{\rm{ \,\text{và}\, y = }}\frac{1}{2}x\)

Bài 2: Vẽ đồ thị hàm số sau:

a) y = 3x; b) y = -3x c) y = \(\frac{1}{2}\)x d) y = \( - \frac{1}{3}\)x.

Bài 3: Tìm giá trị của a trong mỗi trường hợp sau đây.

a. Biết rằng điểm A\(\left( {a; - \frac{7}{5}} \right)\)thuộc đồ thị hàm số \(y = \frac{7}{2}x\).

b. Biết rằng điểm B\(\left( {0,35;b} \right)\)thuộc đồ thị hàm số \(y = \frac{1}{7}x\).

Bài 4: Giả sử A và B là hai điểm thuộc đồ thị hàm số y = 3x + 1

a. Tung độ của điểm A bằng bao nhiêu nếu hoành độ của nó bằng \(\frac{2}{3}\)

b. Hoành độ của điểm B bằng bao nhiêu nếu tung độ của nó bằng -8

Bài 5:

a) Xác định hàm số y = ax biết đồ thị của hàm số đi qua ( 3; 6 )

b) Những điểm nào sau đây thuộc đồ thị hàm số: y = -3x.

A\(\left( { - \frac{1}{3};1} \right)\); B\(\left( { - \frac{1}{3}; - 1} \right)\) ; C\(\left( {0;0} \right)\)

Bài 6:

a) Cho hàm số y =f( x)= -5x -1. Tính f(-1), f(0), f(1), f(\(\frac{1}{2}\))

b) Cho hàm số y = f(x) = -2x + 3. Tính f(-2) ;f(-1) ; f(0) ; f(\( - \frac{1}{2}\)); f(\(\frac{1}{2}\)).

c) Cho hàm số y = g(x) = x² – 1. Tính g(-1); g(0) ; g(1) ; g(2).

Dạng 5: Một số bài tập nâng cao

Bài 1: Cho biểu thức \(A = \frac{1}{3} + \frac{1}{{{3^2}}} + \frac{1}{{{3^3}}} + ...\frac{1}{{{3^{99}}}}.\) Chứng minh \(C < \frac{1}{2}\)

Bài 2: Cho biểu thức: \(D = \frac{1}{2} + {\left( {\frac{1}{2}} \right)^2} + {\left( {\frac{1}{2}} \right)^3} + ... + {\left( {\frac{1}{2}} \right)^{98}} + {\left( {\frac{1}{2}} \right)^{99}}.\) Chứng minh \(D < 1\)

Bài 3: Tính: \(M = {2^{2012}} - \left( {{2^{2011}} + {2^{2010}} + ... + {2^1} + {2^0}} \right)\)

Bài 4: Rút gọn: \(N = {3^{100}} - {3^{99}} + {3^{98}} - {3^{97}} + ... + {3^2} - 3 + 1\)

Bài 5: Tính: \(B = \frac{1}{{100}} - \frac{1}{{100.99}} - \frac{1}{{99.98}} - \frac{1}{{98.97}} - ... - \frac{1}{{3.2}} - \frac{1}{{2.1}}\)

BT tự luận hình học

Bài 1: Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho AC = BD.

a) Chứng minh: AD = BC.

b) Gọi E là giao điểm AD và BC. Chứng minh: \(5\frac{5}{{27}} + \frac{7}{{23}} + 0,5 - \frac{5}{{27}} + \frac{{16}}{{23}}\)EAC = \(5\frac{5}{{27}} + \frac{7}{{23}} + 0,5 - \frac{5}{{27}} + \frac{{16}}{{23}}\)EBD.

c) Chứng minh: OE là phân giác của góc xOy.

Bài 2: Cho \(\Delta \)ABC. Trên tia đối của tia CB lấy điểm M sao cho CM = CB. Trên tia đối của tia CA lấy điểm D sao cho CD = CA

a) Chứng minh \(\Delta \) ABC = \(\Delta \)DMC

b) Chứng minh MD // AB

c) Gọi I là một điểm nằm giữa A và B. Tia CI cắt MD tại điểm N. So sánh độ dài các đoạn thẳng BI và NM, IA và ND

Bài 3: Cho ∆ ABC có AB = AC, kẻ BD ^ AC, CE ^ AB (D thuộc AC, E thuộc AB). Gọi O là giao điểm của BD và CE. Chứng minh:

a) BD = CE

b) ∆OEB = ∆ODC

c) AO là tia phân giác của góc BAC .

Bài 4: Cho\(\Delta ABC\)vuông ở A và AB =AC. Gọi K là trung điểm của BC.

a) Chứng minh: \(\Delta \)AKB =\(\Delta \)AKC

b) Chứng minh: AK\( \bot \) BC

c) Từ C vẽ đường vuông góc với BC cắt đường thẳng AB tại. Chứng minh EC //AK

Bài 5: Cho tam giác ABC có 3 góc đều nhọn, đường cao AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HA = HD.

a) Chứng minh BC và CB lần lượt là các tia phân giác của các góc ABD và ACD.

b) Chứng minh CA = CD và BD = BA.

c) Cho góc ACB = 45⁰.Tính góc ADC.

d) Đường cao AH phải có thêm điều kiện gì thì AB // CD.

Bài 6: Cho tam giác ABC với AB = AC. Lấy I là trung điểm BC. Trên tia BC lấy điểm N, trên tia CB lấy điểm M sao cho CN=BM.

a) Chứng minh \(\widehat {ABI} = \widehat {ACI}\) và AI là tia phân giác góc BAC.

b) Chứng minh AM = AN

c) Chứng minh AI\( \bot \)BC.

Bài 7: Cho tam giác ABC có góc A bằng 90⁰. Đường thẳng AH vuông góc với BC tại. Trên đường vuông góc với BC lấy điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho AH = BD

a) Chứng minh DAHB = DDBH

b) Hai đường thẳng AB và DH có song song không? Vì sao?

c) Tính góc ACB biết góc BAH = 35⁰

Bài 8: Cho tam giác ABC, M, N là trung điểm của AB và AC. trên tia đối của tia NM xác định điểm P sao cho NP = MN. Chứng minh:

a) CP//AB

b) MB = CP

c) BC = 2MN

Bài 9: Cho tam giác ABC vuông tại A có \(\widehat B = {60^0}\) và M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho \(MA = MD\)

a) Tính số đo góc C

b) Chứng minh \(\Delta MAB = \Delta MDC\)

c) Chứng minh AB//CD và \(AC \bot CD\) \(\)

d) Chứng minh: \(BC = 2AM\)

Bài 10: Cho tam giác ABC, E là trung điểm của BC. Lấy D thuộc tia đối của tia EA sao cho ED=EA.

a) Chứng minh rằng: \(\Delta AEB = \Delta DEC\)

b) Chứng minh rằng: AC // BD

c) Kẻ \(EI \bot AC\,\,\left( {I \in AC} \right)\,;\,EK \bot BD\,\left( {K \in BD} \right)\) Chứng minh \(\Delta AIE = \Delta DKE\)

d) Chứng minh 3 điểm I, E, K thẳng hàng.