Câu hỏi
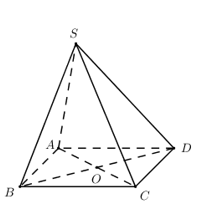
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(2a,\,AC = \sqrt 3 a,\,SAB\) là tam giác đều, \(\angle SAD = {120^0}.\) Tính thể tích của khối chóp \(S.ABCD.\)
- A \(\sqrt 3 {a^3}\)
- B \(\dfrac{{3\sqrt 3 {a^3}}}{2}\)
- C \(\sqrt 6 {a^3}\)
- D \(\dfrac{{2\sqrt 3 {a^3}}}{3}\)
Phương pháp giải:
Sử dụng công thức tính nhanh chóp \(S.ABC\) khi biết \(SA = a,\,\,SB = b,\,\,SC = c,\) \(\angle ASB = \alpha ,\,\,\angle BSC = \beta ,\,\,\angle CSA = \gamma \) là :
\(V = \dfrac{1}{6}abc\sqrt {1 + 2\cos \alpha cos\beta cos\gamma - \left( {\cos {\alpha ^2} + cos{\beta ^2} + co{s^2}\gamma } \right)} \)
Lời giải chi tiết:
Tam giác \(SAB\) đều \( \Rightarrow SA = SB = AB = 2a\).
Áp dụng định lí Cosin trong tam giác \(ABC\) ta có:
\(\cos \angle BAC = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}} = \dfrac{{4{a^2} + 3{a^2} - 4{a^2}}}{{2.2a.a\sqrt 3 }} = \dfrac{{\sqrt 3 }}{4}\)
\( \Rightarrow \cos \angle BAD = 2{\cos ^2}\angle BAC - 1 = 2.\dfrac{3}{{16}} - 1 = - \dfrac{5}{8}\).
Ta có \({S_{ABCD}} = 2{S_{ABD}} \Rightarrow {V_{S.ABCD}} = {V_{S.ABD}} = {V_{A.SBD}}\)
Sử dụng công thức tính nhanh chóp \(A.SBD\) khi biết \(AS = 2a,\,\,AB = 2a,\,\,AD = 2a,\) \(\angle SAB = {60^0},\,\,\angle SAD = {120^0},\,\,\cos \angle BAD = - \dfrac{5}{8}\) là :
\({V_{A.SBD}} = \dfrac{1}{6}.2a.2a.2a\sqrt {1 + 2\dfrac{1}{2}.\dfrac{{ - 1}}{2}.\dfrac{{ - 5}}{8} - \left( {\dfrac{1}{4} + \dfrac{1}{4} + \dfrac{{25}}{{64}}} \right)} = \dfrac{{8{a^3}}}{6}.\dfrac{{3\sqrt 3 }}{8} = \dfrac{{\sqrt 3 {a^3}}}{2}\).
Vậy \({V_{S.ABCD}} = 2{V_{A.SBD}} = 2.\dfrac{{\sqrt 3 {a^3}}}{2} = \sqrt 3 {a^3}\).
Chọn A.