Phương pháp giải:

- Tìm tập hợp điểm biểu diễn số phức thỏa mãn \(\left| {z - 5 - 3i} \right| = 5\).

- Gọi \({M_1},{M_2}\) là các điểm biểu diễn số phức \({z_1},{z_2}\) suy ra điều kiện của \({M_1}{M_2}\) và tập hợp điểm biểu diễn số phức \(w\).

Lời giải chi tiết:

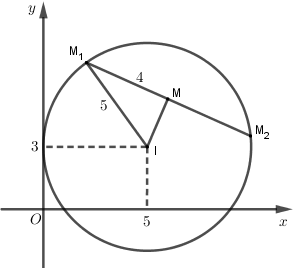
Tập hợp điểm biểu diễn số phức \(z = x + yi\) thỏa mãn \(\left| {z - 5 - 3i} \right| = 5\) là đường tròn tâm \(I\left( {5;3} \right)\) bán kính \(R = 5\).

Gọi \({M_1}\left( {{x_1};{y_1}} \right),{M_2}\left( {{x_2};{y_2}} \right)\) là hai điểm biểu diễn các số phức \({z_1},{z_2}\) thì từ \(\left| {{z_1} - {z_2}} \right| = 8\) ta suy ra \({M_1}{M_2} = 8\).

Tập hợp điểm biểu diễn số phức \(z = x + yi\) thỏa mãn \(\left| {z - 5 - 3i} \right| = 5\) là đường tròn tâm \(I\left( {5;3} \right)\) bán kính \(R = 5\).

Gọi \({M_1}\left( {{x_1};{y_1}} \right),{M_2}\left( {{x_2};{y_2}} \right)\) là hai điểm biểu diễn các số phức \({z_1},{z_2}\) thì từ \(\left| {{z_1} - {z_2}} \right| = 8\) ta suy ra \({M_1}{M_2} = 8\).

Gọi \(N\left( {x;y} \right)\) là điểm biểu diễn số phức \(w = {z_1} + {z_2}\) thì \(\left\{ \begin{array}{l}x = {x_1} + {x_2}\\y = {y_1} + {y_2}\end{array} \right.\).

Gọi \(M\) là trung điểm \({M_1}{M_2}\) thì \(M\left( {\dfrac{{{x_1} + {x_2}}}{2};\dfrac{{{y_1} + {y_2}}}{2}} \right)\).

Ta có: \(IM = \sqrt {IM_1^2 - {M_1}{M^2}}  = \sqrt {{5^2} - {4^2}}  = 3\) hay \(\sqrt {{{\left( {\dfrac{{{x_1} + {x_2}}}{2} - 5} \right)}^2} + {{\left( {\dfrac{{{y_1} + {y_2}}}{2} - 3} \right)}^2}}  = 3\)\( \Leftrightarrow {\left( {\dfrac{{{x_1} + {x_2}}}{2} - 5} \right)^2} + {\left( {\dfrac{{{y_1} + {y_2}}}{2} - 3} \right)^2} = 9\)\( \Leftrightarrow {\left[ {\left( {{x_1} + {x_2}} \right) - 10} \right]^2} + {\left[ {\left( {{y_1} + {y_2}} \right) - 6} \right]^2} = 36\)\( \Leftrightarrow {\left( {x - 10} \right)^2} + {\left( {y - 6} \right)^2} = 36\)

Vậy tập hợp các điểm \(N\) thỏa mãn bài toán là đường tròn \({\left( {x - 10} \right)^2} + {\left( {y - 6} \right)^2} = 36\).

Chọn A.