Phương pháp giải:

+) Tính đạo hàm \(y'\)

+) Để hàm số đồng biến trên  khoảng \(K\) thì \(y' \ge 0;\,\forall x \in K\)

+) Cô lập \(m\) đưa về dạng \(g\left( x \right) \ge m;\,\forall x \in K\) từ đó suy ra \(m.\)

Lời giải chi tiết:

ĐK : \(x \ne 1\)

Ta có \(y' = \dfrac{{\left[ {2\left( {m + 1} \right)x - 2m} \right].\left( {x - 1} \right) - \left( {m + 1} \right){x^2} + 2mx - 6m}}{{{{\left( {x - 1} \right)}^2}}}\)

            \(\begin{array}{l} = \dfrac{{2\left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x - 2mx + 2m - \left( {m + 1} \right){x^2} + 2mx - 6m}}{{{{\left( {x - 1} \right)}^2}}}\\ = \dfrac{{\left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x - 4m}}{{{{\left( {x - 1} \right)}^2}}}\end{array}\)

Để hàm số đồng biến trên \(\left( {4; + \infty } \right)\) thì \(y' \ge 0;\,\forall x > 4\)

\( \Rightarrow \left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x - 4m \ge 0  ;\,\forall x > 4\)

\( \Leftrightarrow \left( {m + 1} \right)\left( {{x^2} - 2x} \right) \ge 4m;\,\forall x > 4\)

+ Với \(m + 1 = 0 \Leftrightarrow m =  - 1 \Rightarrow 0 >  - 4\,\,\,\left( {luon\,\,dung} \right)\) nên nhận \(m =  - 1.\) (1)

+ Với \(m + 1 > 0 \Leftrightarrow m >  - 1 \Rightarrow {x^2} - 2x \ge \dfrac{{4m}}{{m + 1}};\,\forall x > 4 \Leftrightarrow \dfrac{{4m}}{{m + 1}} \le \mathop {\min }\limits_{\left[ {4; + \infty } \right)} \left( {{x^2} - 2x} \right)\)

Xét hàm số \(g\left( x \right) = {x^2} - 2x\)có \(g'\left( x \right) = 2x - 2 = 0 \Leftrightarrow x = 1 \notin \left( {4; + \infty } \right)\), ta có BBT trên \(\left( {4; + \infty } \right)\) là

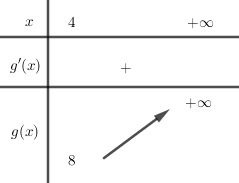
Từ BBT suy ra \(\left\{ \begin{array}{l}\dfrac{{4m}}{{m + 1}} \le 8\\m >  - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4m \le 8m + 8\\m >  - 1\end{array} \right. \ge \left\{ \begin{array}{l}m \ge  - 2\\m >  - 1\end{array} \right. \Leftrightarrow m >  - 1\)  (2)

+ Với \(m + 1 < 0 \Leftrightarrow m <  - 1 \Rightarrow {x^2} - 2x \le \dfrac{{4m}}{{m + 1}};\,\forall x > 4 \Rightarrow \dfrac{{4m}}{{m + 1}} \ge \mathop {\max }\limits_{\left( {4; + \infty } \right)} g\left( x \right)\).

Từ BBT của \(g\left( x \right)\) suy ra không có \(m\) thỏa mãn.

Từ (1) và (2) suy ra \(m \ge  - 1\) mà \(m \in \left[ { - 2019;2019} \right]\) và \(m\) nguyên nên \(m \in \left\{ { - 1;0;...;2019} \right\} \Rightarrow \) có \(2021\) số thỏa mãn.

Chọn D