Phương pháp giải:

- Lập hàm tinh thể tích khối nón, xét hàm suy ra GTLN.

- Tính diện tích \(S,S'\) với chú ý \(S\) là diện tích hình tròn và \(S'\) là diện tích xung quanh của hình nón

Lời giải chi tiết:

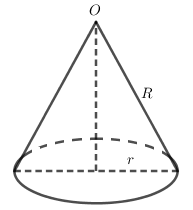
Diện tích hình tròn \(S = \pi {R^2}\).

Gọi bán kính đường tròn đáy hình nón là \(r\,\,\left( {0 < r < R} \right)\) ta có \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {r^2}\sqrt {{R^2} - {r^2}} \).

Xét hàm \(f\left( r \right) = {r^2}\sqrt {{R^2} - {r^2}} \) có \(f'\left( r \right) = 2r\sqrt {{R^2} - {r^2}}  + {r^2}.\dfrac{{ - r}}{{\sqrt {{R^2} - {r^2}} }} = \dfrac{{2r\left( {{R^2} - {r^2}} \right) - {r^3}}}{{\left( {{R^2} - {r^2}} \right)\sqrt {{R^2} - {r^2}} }} = \dfrac{{r\left( {2{R^2} - 3{r^2}} \right)}}{{\left( {{R^2} - {r^2}} \right)\sqrt {{R^2} - {r^2}} }}\)

\(f'\left( r \right) = 0 \Leftrightarrow r = \dfrac{{R\sqrt 2 }}{{\sqrt 3 }}\) (do \(0 < r < R\)).

Bảng biến thiên:

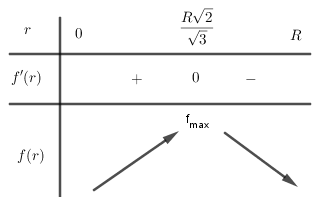
Do đó thể tích \(V\) đạt GTLN tại \(r = \dfrac{{R\sqrt 2 }}{{\sqrt 3 }}\). Khi đó \(S' = {S_{xq}} = \pi rl = \pi .\dfrac{{R\sqrt 2 }}{{\sqrt 3 }}.R = \dfrac{{\pi {R^2}\sqrt 2 }}{{\sqrt 3 }}\).

Vậy \(\dfrac{{S'}}{S} = \dfrac{{\pi {R^2}\sqrt 2 }}{{\sqrt 3 }}:\pi {R^2} = \dfrac{{\sqrt 2 }}{{\sqrt 3 }} = \dfrac{{\sqrt 6 }}{3}\).

Chọn D