Câu hỏi
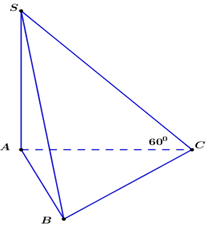
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đề cạnh bằng \(a,\)cạnh bên \(SA\) vuông góc với đáy. Biết rằng đường thẳng \(SC\) hợp với mặt phẳng đáy một góc \({60^0}.\) Thể tích của khối chóp \(S.ABC\) bằng
- A \(\frac{{{a^3}}}{8}\)
- B \(\frac{{{a^3}}}{2}\)
- C \(\frac{{{a^3}}}{4}\)
- D \(\frac{{3{a^3}}}{4}\)
Phương pháp giải:
Công thức tính thể tích khối chóp có diện tích đáy \(S\) và chiều cao \(h\) là: \(V = \frac{1}{3}Sh.\)
Lời giải chi tiết:
Ta có:\(SA \bot \left( {ABC} \right)\)
\( \Rightarrow \angle \left( {SC,\,\,\left( {ABC} \right)} \right) = \angle \left( {SA,\,SC} \right) = \angle SCA = {60^0}\)
Xét \(\Delta SAC\) ta có: \(SA = AC.\tan {60^0} = a\sqrt 3 .\)
\( \Rightarrow V = \frac{1}{3}SA.{S_{ABC}} = \frac{1}{3}.a\sqrt 3 .\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}}}{4}.\)
Chọn C.
Câu hỏi trước
