Phương pháp giải:

+) Lập BBT của đồ thị hàm số \(y = f\left( x \right)\).

+) Xét dấu đạo hàm của hàm số \(y = {\left( {f\left( x \right)} \right)^2}\) và kết luận các khoảng đơn điệu của hàm số trên các khoảng đáp án cho

Lời giải chi tiết:

Từ đồ thị hàm số \(y = f'\left( x \right)\) ta suy ra BBT của đồ thị hàm số \(y = f\left( x \right)\) như sau :

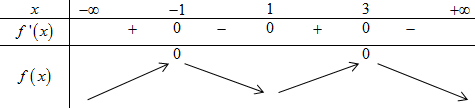
Đặt \(y = g\left( x \right) = {\left( {f\left( x \right)} \right)^2}\) ta có

\(y' = g'\left( x \right) = 2f\left( x \right)f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 0\\f'\left( x \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - 1\,\,\left( {boi\,\,2} \right)\\x = 3\,\,\left( {boi\,\,2} \right)\\x = 1\,\,\left( {boi\,\,1} \right)\end{array} \right.\)

 Do đó \(x = 1\) là 1 cực trị của hàm số, do đó loại các đáp án C và D.

Xét đáp án A ta có \(\forall x \in \left( {1;2} \right) \Rightarrow \left\{ \begin{array}{l}f\left( x \right) < 0\\f'\left( x \right) > 0\end{array} \right. \Rightarrow g'\left( x \right) < 0 \Rightarrow \) Hàm số \(y = g\left( x \right)\) nghịch biến trên \(\left( {1;2} \right)\).

Chọn A.