Phương pháp giải:

Xác định dạng của đồ thị hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,\left( {a \ne 0} \right)\) từ đó suy ra đồ thị hàm số \(y = \left| {a{x^3} + b{x^2} + cx + d} \right|\) và suy ra số cực trị của nó.

Lời giải chi tiết:

Phương trình \(a{x^3} + b{x^2} + cx + d = 0\,\,\left( {a \ne 0} \right)\) có 2 nghiệm thực nên đồ thị hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,\left( {a \ne 0} \right)\) dạng :

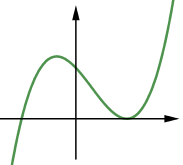 hoặc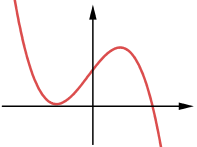 

Vậy số cực trị của hàm số \(y = \left| {a{x^3} + b{x^2} + cx + d} \right|\) là 3.

Chọn B.