Phương pháp giải:

+) Xác định tâm mặt cầu ngoại tiếp chóp là giao điểm của trục của mặt đáy và mặt phẳng trung trực của 1 cạnh bên.

+) Áp dụng các kiến thức đã học tính bán kính mặt cầu. Từ đó áp dụng công thức tính diện tích mặt cầu bán kính $R:\;\;S = 4\pi {R^2}.$

Lời giải chi tiết:

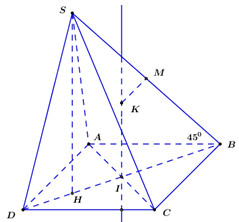
Gọi H  là trung điểm của ID \( \Rightarrow SH \bot \left( {ABCD} \right).\)

Qua I dựng đường thẳng d song song với SH,  đường thẳng này chính là trục của hình chóp SABCD.

Dựng đường thẳng trung trực của cạnh SB, cắt đường thẳng d tại K.

Khi đó K là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.  

Ta có: \(\angle \left( {SB,\,\,\left( {ABCD} \right)} \right) = \angle \left( {SB,\,\,BH} \right) = \angle SBH = {45^0}.\)

         \(BD = 5a \Rightarrow BH = \dfrac{3}{4}BD = \dfrac{{15a}}{4} = SH \Rightarrow SB = BH\sqrt 2  = \dfrac{{15a\sqrt 2 }}{4}\).

Gọi \(E = d \cap SB\). Áp dụng định lí Ta-lét ta có: \(\dfrac{{IE}}{{AH}} = \dfrac{{IB}}{{BH}} = \dfrac{2}{3} \Leftrightarrow IE = \dfrac{2}{3}SH = \dfrac{{5a}}{2}\).

\(\dfrac{{EB}}{{SB}} = \dfrac{{IB}}{{HB}} = \dfrac{2}{3} \Rightarrow EB = \dfrac{2}{3}SB = \dfrac{{5a\sqrt 2 }}{2};\,\,AM = MB = \dfrac{1}{2}SB = \dfrac{{15a\sqrt 2 }}{8}\).

\( \Rightarrow EM = EB - MB = \dfrac{{5a\sqrt 2 }}{8}\).

\(\angle SBH = {45^0} \Rightarrow \angle MEK = {45^0} \Rightarrow \Delta EMK\) vuông cân tại \(M \Rightarrow MK = ME = \dfrac{{5a\sqrt 2 }}{8}\).

Áp dụng định lí Pytago trong tam giác vuông \(MBK\) ta có :

\(KB = \sqrt {K{M^2} + M{B^2}}  = \sqrt {\dfrac{{25{a^2}}}{{32}} + \dfrac{{225{a^2}}}{{32}}}  = \dfrac{{5\sqrt 5 a}}{4} = R\).

Vậy diện tích mặt cầu ngoại tiếp chóp \(S.ABCD\) là \(S = 4\pi {R^2} = \dfrac{{125\pi }}{4}{a^2}\).

Chọn D.