Phương pháp giải:

- Tính các giá trị \(f\left( 0 \right),f\left( 1 \right),f\left( 2 \right)\) và nhận xét suy ra bảng biến thiên của \(y = f\left( x \right)\).

- Từ đó suy ra bảng biến thiên của \(y = f\left( {\left| x \right|} \right)\) và \(y = \left| {f\left( {\left| x \right|} \right)} \right|\).

Lời giải chi tiết:

\(\begin{array}{l}f\left( x \right) = {x^3} + m{x^2} + nx - 1\\f\left( 0 \right) =  - 1 < 0\\f\left( 1 \right) = m + n > 0\\f\left( 2 \right) = 7 + 2\left( {2m + n} \right) < 0\\f'\left( x \right) = 3{x^2} + 2mx + n\\\Delta ' = {m^2} - 3n\end{array}\)

Các số \(f\left( 0 \right),f\left( 1 \right),f\left( 2 \right)\) thay đổi tính âm dương nên hàm số phải có 3 nghiệm.

Ta có các bảng biến thiên sau

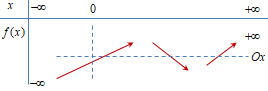
Chỗ \(x = 0\) không thể là cực trị do \(f'\left( 0 \right) = n \ne 0,\) vì nếu \(n=0\) thế vào điều kiện ban đầu ta có \(\left\{ \begin{array}{l}m > 0\\7 + 4m < 0\end{array} \right.\) (vô lí).

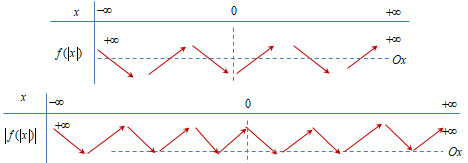
Hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|\) có 11 điểm cực trị.

Chọn B.