Phương pháp giải:

+ TXĐ

+ Tính \(f'\left( x \right)\), giải phương trình \(f'\left( x \right) = 0\). Lập BBT trên khoảng \(\left( {0; + \infty } \right)\)

+ Dựa vào BBT tìm GTNN của hàm số trên \(\left( {0; + \infty } \right)\)

Lời giải chi tiết:

Hàm số xác định và liên tục trên khoảng \(\left( {0; + \infty } \right)\).

Ta có \({f}'\left( x \right)=1-\dfrac{1}{{{x}^{2}}}=\dfrac{{{x}^{2}}-1}{{{x}^{2}}}\).

\(f'\left( x \right) = 0 \Leftrightarrow \dfrac{{{x^2} - 1}}{{{x^2}}} = 0 \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\,\,\,\,\,\,\left( {tm} \right)\\x =  - 1\,\,\left( {ktm} \right)\end{array} \right.\). (Vì xét trên khoảng \(\left( {0; + \infty } \right)\))

Ta có BBT của hàm số trên \(\left( 0;+\infty  \right)\).

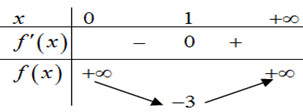
Từ BBT suy ra \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} f\left( x \right) =  - 3\) khi \(x = 1.\)

Chọn A.