Câu hỏi
Cho hàm số \(f\left( x \right)\) với bảng biến thiên dưới đây:
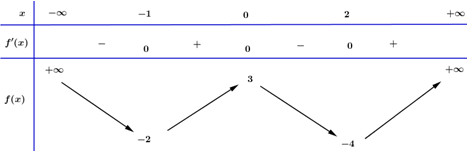
Hỏi hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|\) có bao nhiêu cực trị?
- A 5
- B 3
- C 1
- D 7
Phương pháp giải:
Cách 1: Dựa vào BBT, vẽ BBT của đồ thị hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|\) và suy ra số các điểm cực trị của hàm số.
Cách 2: Từ BBT suy ra công thức hàm số \(y = f\left( x \right)\) từ đó vẽ đồ thị hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|\) và suy ra số các điểm cực trị của hàm số.
Lời giải chi tiết:
Dựa vào BBT ta thấy hàm số \(y = f\left( x \right)\) có 3 điểm cực trị \(\left( { - 1;\, - 2} \right),\,\,\left( {0;\,\,3} \right),\,\,\left( {2; - 4} \right)\)
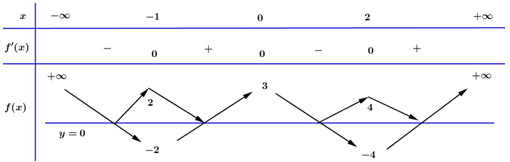
Khi đó ta có BBT của hàm số \(y = \left| {f\left( x \right)} \right|\) như sau:
BBT của hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|\) là:
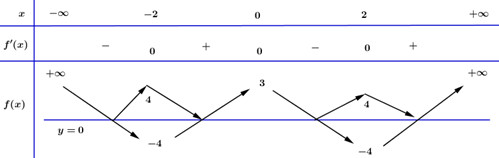
Như vậy hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|\) có 7 điểm cực trị.
Chọn D.







