Phương pháp giải:

+ Tính cạnh của hình lập phương

+ Hình lập phương cạnh \(a\) có bán kính mặt cầu ngoại tiếp là \(R = \frac{{a\sqrt 3 }}{2}\)

+ Diện tích mặt cầu bán kính \(R\) là \(S = 4\pi {R^2}\)

+ Thể tích mặt cầu bán kính \(R\) là \(V = \frac{4}{3}\pi {R^3}\)

Lời giải chi tiết:

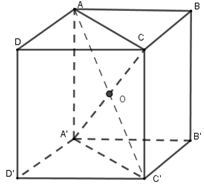
Gọi hình lập phương \(ABCD.A'B'C'D'\) cạnh \(x\) có diện tích mặt chéo \({S_{ACC'A'}} = {a^2}\sqrt 2 \)

Ta có \(AC = \sqrt {A{D^2} + D{C^2}}  = x\sqrt 2 \)  nên \({S_{ACC'A'}} = AC.AA' = x\sqrt 2 .x = {a^2}\sqrt 2  \Rightarrow x = a\)

Bán kính mặt cầu ngoại tiếp hình lập phương là \(R = \frac{{a\sqrt 3 }}{2}\)

Nên thể tích khối cầu ngoại tiếp hình lập phương là \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {\left( {\frac{{a\sqrt 3 }}{2}} \right)^3} = \frac{{\sqrt 3 \pi {a^3}}}{2}\)

Diện tích mặt cầu ngoại tiếp hình lập phương là \(S = 4\pi {R^2} = 4\pi .{\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = 3\pi {a^2}\)

Suy ra \(S.V = 3\pi {a^3}.\frac{{\sqrt 3 }}{2}\pi {a^3} = \frac{{3\sqrt 3 }}{2}{\pi ^2}{a^5}\)

Chọn B.